题目内容
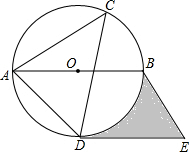 (2013•本溪)如图,⊙O是△ACD的外接圆,AB是直径,过点D作直线DE∥AB,过点B作直线BE∥AD,两直线交于点E,如果∠ACD=45°,⊙O的半径是4cm
(2013•本溪)如图,⊙O是△ACD的外接圆,AB是直径,过点D作直线DE∥AB,过点B作直线BE∥AD,两直线交于点E,如果∠ACD=45°,⊙O的半径是4cm(1)请判断DE与⊙O的位置关系,并说明理由;
(2)求图中阴影部分的面积(结果用π表示).
分析:(1)连结OD,根据圆周角定理得∠ABD=∠ACD=45°,∠ADB=90°,可判断△ADB为等腰直角三角形,所以OD⊥AB,而DE∥AB,则有OD⊥DE,然后根据切线的判定定理得到DE为⊙O的切线;
(2)先由BE∥AD,DE∥AB得到四边形ABED为平行四边形,则DE=AB=8cm,然后根据梯形的面积公式和扇形的面积公式利用S阴影部分=S梯形BODE-S扇形OBD
进行计算即可.
(2)先由BE∥AD,DE∥AB得到四边形ABED为平行四边形,则DE=AB=8cm,然后根据梯形的面积公式和扇形的面积公式利用S阴影部分=S梯形BODE-S扇形OBD
进行计算即可.
解答: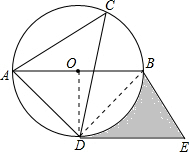 解:(1)DE与⊙O相切.理由如下:
解:(1)DE与⊙O相切.理由如下:
连结OD,BD,则∠ABD=∠ACD=45°,
∵AB是直径,
∴∠ADB=90°,
∴△ADB为等腰直角三角形,
∵点O为AB的中点,
∴OD⊥AB,
∵DE∥AB,
∴OD⊥DE,
∵OD是半径,
∴DE为⊙O的切线;
(2)∵BE∥AD,DE∥AB,
∴四边形ABED为平行四边形,
∴DE=AB=8cm,
∴S阴影部分=S梯形BODE-S扇形OBD
=
(4+8)×4-
=(24-4π)cm2.
 解:(1)DE与⊙O相切.理由如下:
解:(1)DE与⊙O相切.理由如下:连结OD,BD,则∠ABD=∠ACD=45°,
∵AB是直径,
∴∠ADB=90°,
∴△ADB为等腰直角三角形,
∵点O为AB的中点,
∴OD⊥AB,
∵DE∥AB,
∴OD⊥DE,
∵OD是半径,
∴DE为⊙O的切线;
(2)∵BE∥AD,DE∥AB,
∴四边形ABED为平行四边形,
∴DE=AB=8cm,
∴S阴影部分=S梯形BODE-S扇形OBD
=
| 1 |
| 2 |
| 90•π•42 |
| 360 |
=(24-4π)cm2.
点评:本题考查了圆的切线的判定:过半径的外端点与半径垂直的直线为圆的切线.也考查了圆周角定理和扇形的面积公式.

练习册系列答案
相关题目
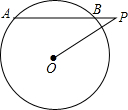 (2013•本溪)如图,⊙O的半径是3,点P是弦AB延长线上的一点,连接OP,若OP=4,∠APO=30°,则弦AB的长为( )
(2013•本溪)如图,⊙O的半径是3,点P是弦AB延长线上的一点,连接OP,若OP=4,∠APO=30°,则弦AB的长为( ) (2013•本溪)如图放置的圆柱体的左视图为( )
(2013•本溪)如图放置的圆柱体的左视图为( )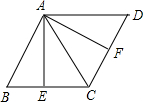 (2013•本溪)如图,在菱形ABCD中,∠BAD=2∠B,E,F分别为BC,CD的中点,连接AE、AC、AF,则图中与△ABE全等的三角形(△ABE除外)有( )
(2013•本溪)如图,在菱形ABCD中,∠BAD=2∠B,E,F分别为BC,CD的中点,连接AE、AC、AF,则图中与△ABE全等的三角形(△ABE除外)有( ) (2013•本溪)如图,在矩形OABC中,AB=2BC,点A在y轴的正半轴上,点C在x轴的正半轴上,连接OB,反比例函数y=
(2013•本溪)如图,在矩形OABC中,AB=2BC,点A在y轴的正半轴上,点C在x轴的正半轴上,连接OB,反比例函数y=