题目内容
顶点为P的抛物线y=x2-2x+3与y轴相交于点A,在顶点不变的情况下,把该抛物线绕顶点P旋转180°得到一个新的抛物线,且新的抛物线与y轴相交于点B,则△PAB的面积为
- A.1
- B.2
- C.3
- D.6
A
分析:根据题目意思,求出A和B的坐标,再求三角形的面积则可.
解答:当x=0时,y=3,所以A的坐标是(0,3),y=x2-2x+3=(x-1)2+2,
把它绕顶点P旋转180°得到一个新的抛物线是y=-(x-1)2+2=-x2+2x+1,x=0时,y=1,所以B的坐标是(0,1),P的坐标是(1,2),△PAB的面积= ×2×(3-2)=1.
×2×(3-2)=1.
故选A.
点评:本题考查了抛物线与坐标轴交点的求法,和考查抛物线将一般式转化顶点式的能力,难度较大.
分析:根据题目意思,求出A和B的坐标,再求三角形的面积则可.
解答:当x=0时,y=3,所以A的坐标是(0,3),y=x2-2x+3=(x-1)2+2,
把它绕顶点P旋转180°得到一个新的抛物线是y=-(x-1)2+2=-x2+2x+1,x=0时,y=1,所以B的坐标是(0,1),P的坐标是(1,2),△PAB的面积=
 ×2×(3-2)=1.
×2×(3-2)=1.故选A.
点评:本题考查了抛物线与坐标轴交点的求法,和考查抛物线将一般式转化顶点式的能力,难度较大.

练习册系列答案
相关题目
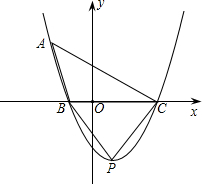 如图,已知顶点为P的抛物线
如图,已知顶点为P的抛物线
 (2013•甘井子区一模)如图,顶点为D的抛物线y=a(x-5)2-6经过点A(
(2013•甘井子区一模)如图,顶点为D的抛物线y=a(x-5)2-6经过点A(