题目内容
 (2013•甘井子区一模)如图,顶点为D的抛物线y=a(x-5)2-6经过点A(
(2013•甘井子区一模)如图,顶点为D的抛物线y=a(x-5)2-6经过点A(| 13 | 2 |
(1)求抛物线和直线CD解析式;
(2)在直线CD右侧的抛物线上取点E,使得∠EDB=∠CBO,则求点E坐标;
(3)点P为射线CD上一点,在(2)条件下,作射线PE,以P为旋转中心逆时针旋转PE,使得旋转后的射线交x坐标轴于点R,且∠EPR=∠CBO.是否存在点R,使得PE=PR?如果存在,请直接写出点R坐标;不存在,则说明理由.
分析:(1)将点A(
,-5)代入y=a(x-5)2-6,求出a=
,即可得到抛物线的解析式;设直线CD解析式为y=kx+b,将D(5,-6),C(0,4)两点的坐标代入,运用待定系数法即可求出直线CD的解析式;
(2)延长DE交x轴于点M,作DH⊥x轴于点H.先证明∠EDB=∠MBD,得出MB=MD,设点M的坐标为(t,0),由于B(2,0),D(5,-6),所以t-2=
,解方程求出t=
,得到M点的坐标为(
,0),运用待定系数法求出DM的解析式为y=
x-
,由于点E为直线DM和抛物线的交点,解方程组
,即可求出点E坐标;
(3)设R(m,0).先根据两点间的距离公式求得DE=5,利用AAS证明△BRP≌△DPE,得出BP=DE=5,BR=DP,再根据两点间的距离公式求得BD=3
,则BR=PD=3
-5,由BR=DP得出方程m-2=3
-5,解方程求出m的值,得到点R坐标,由此得出结论:在(2)条件下,存在点R,能够使得PE=PR.
| 13 |
| 2 |
| 4 |
| 9 |
(2)延长DE交x轴于点M,作DH⊥x轴于点H.先证明∠EDB=∠MBD,得出MB=MD,设点M的坐标为(t,0),由于B(2,0),D(5,-6),所以t-2=
| (t-5)2+36 |
| 19 |
| 2 |
| 19 |
| 2 |
| 4 |
| 3 |
| 38 |
| 3 |
|
(3)设R(m,0).先根据两点间的距离公式求得DE=5,利用AAS证明△BRP≌△DPE,得出BP=DE=5,BR=DP,再根据两点间的距离公式求得BD=3
| 5 |
| 5 |
| 5 |
解答:解:(1)将点A(
,-5)代入y=a(x-5)2-6,
得-5=a(
-5)2-6,解得a=
,
所以抛物线解析式为:y=
(x-5)2-6,即y=
x2-
x+
;
设直线CD解析式为y=kx+b,
∵D(5,-6),C(0,4),
∴
,解得
,
∴直线CD解析式为y=-2x+4;
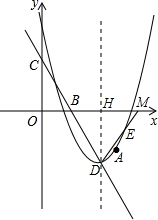 (2)延长DE交x轴于点M,作DH⊥x轴于点H.
(2)延长DE交x轴于点M,作DH⊥x轴于点H.
∵∠EDB=∠CBO,∠CBO=∠MBD,
∴∠EDB=∠MBD,
∴MB=MD.
设点M的坐标为(t,0),
y=-2x+4,当y=0时,x=2,
∴B(2,0),
∴MB=t-2.
在Rt△DHM中,MD=
,
∴t-2=
,
解得:t=
,
∴M(
,0).
设DM解析式为:y=mx+n,
则
,解得
,
∴y=
x-
.
点E为直线DM和抛物线的交点,
由
,解得:
或
,
∴E(8,-2);
 (3)存在,点R坐标为(3
(3)存在,点R坐标为(3
-3,0).理由如下:
设R(m,0).
∵D(5,-6),E(8,-2),
∴DE=
=5.
∵∠EPR=∠CBO=∠MBD,
又∠EPR+∠EPD=∠MBD+∠BRP,
∴∠BRP=∠EPD,
又∠MBD=∠BDE,PR=PE,
∴△BRP≌△DPE,
∴BP=DE=5,BR=DP.
∵B(2,0),D(5,-6),
∴BD=
=3
,
∴PD=BD-BP=3
-5,
∴BR=PD=3
-5,
∴m-2=3
-5,
∴m=3
-3,
∴点R坐标为(3
-3,0).
| 13 |
| 2 |
得-5=a(
| 13 |
| 2 |
| 4 |
| 9 |
所以抛物线解析式为:y=
| 4 |
| 9 |
| 4 |
| 9 |
| 40 |
| 9 |
| 46 |
| 9 |
设直线CD解析式为y=kx+b,
∵D(5,-6),C(0,4),
∴
|
|
∴直线CD解析式为y=-2x+4;
 (2)延长DE交x轴于点M,作DH⊥x轴于点H.
(2)延长DE交x轴于点M,作DH⊥x轴于点H.∵∠EDB=∠CBO,∠CBO=∠MBD,
∴∠EDB=∠MBD,
∴MB=MD.
设点M的坐标为(t,0),
y=-2x+4,当y=0时,x=2,
∴B(2,0),
∴MB=t-2.
在Rt△DHM中,MD=
| (t-5)2+36 |
∴t-2=
| (t-5)2+36 |
解得:t=
| 19 |
| 2 |
∴M(
| 19 |
| 2 |
设DM解析式为:y=mx+n,
则
|
|
∴y=
| 4 |
| 3 |
| 38 |
| 3 |
点E为直线DM和抛物线的交点,
由
|
|
|
∴E(8,-2);
 (3)存在,点R坐标为(3
(3)存在,点R坐标为(3| 5 |
设R(m,0).
∵D(5,-6),E(8,-2),
∴DE=
| (8-5)2+(-2+6)2 |
∵∠EPR=∠CBO=∠MBD,
又∠EPR+∠EPD=∠MBD+∠BRP,
∴∠BRP=∠EPD,
又∠MBD=∠BDE,PR=PE,
∴△BRP≌△DPE,
∴BP=DE=5,BR=DP.
∵B(2,0),D(5,-6),
∴BD=
| (5-2)2+(-6-0)2 |
| 5 |
∴PD=BD-BP=3
| 5 |
∴BR=PD=3
| 5 |
∴m-2=3
| 5 |
∴m=3
| 5 |
∴点R坐标为(3
| 5 |
点评:本题是二次函数的综合题型,其中涉及到运用待定系数法求一次函数、二次函数的解析式,函数图象上点的坐标特征,全等三角形的判定与性质,两函数交点坐标的求法,旋转的性质,两点间的距离公式等知识,综合性较强,有一定难度.运用数形结合、方程思想是解题的关键.

练习册系列答案
相关题目
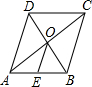 (2013•甘井子区二模)如图,在菱形ABCD中,对角线AC,BD相交于点O,E为AB的中点,且OE=a,则菱形ABCD的周长为
(2013•甘井子区二模)如图,在菱形ABCD中,对角线AC,BD相交于点O,E为AB的中点,且OE=a,则菱形ABCD的周长为