题目内容
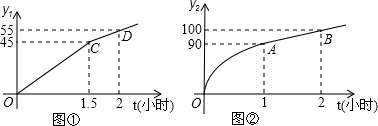
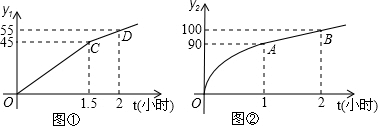
科学研究表明,合理安排各学科的课外学习时间,可以有效的提高学习的效率.教育专家们通过对九年级学生的课外学习时间与学习收益情况进行进一步的研究发现,九年级学生每天课外用于非数学学科的学习时间t(小时)与学习收益量y1的函数关系是图①中的一条折线;每天用于数学学科的学习时间t(小时)与学习收益量y2的函数关系如图②所示:图象中OA是顶点为A的抛物线的一部分,AB是射线.
(1)求出y1与时间t(小时)之间的函数关系式,并注明自变量t的取值范围;
(2)求出y2与时间t(小时)之间的函数关系式,并注明自变量t的取值范围;
(3)如果九年级学生每天课外学习的时间为2小时,学习的总收益量为W(W=y1+y2),请问应如何安排学习时间才能使学习的总收益量最大?

(1)求出y1与时间t(小时)之间的函数关系式,并注明自变量t的取值范围;
(2)求出y2与时间t(小时)之间的函数关系式,并注明自变量t的取值范围;
(3)如果九年级学生每天课外学习的时间为2小时,学习的总收益量为W(W=y1+y2),请问应如何安排学习时间才能使学习的总收益量最大?
分析:(1)由图以及t的取值范围,设直线解析式为y=kx以及y=ax+b利用图象上点的坐标,即可求出y与x的函数关系式;
(2)利用分段函数的知识,需要注意的是x的取值范围依照分段函数的解法求抛物线解析式和直线解析式解出即可;
(3)根据W=y1+y2,分别根据二次函数最值求法以及t的取值范围求出即可.
(2)利用分段函数的知识,需要注意的是x的取值范围依照分段函数的解法求抛物线解析式和直线解析式解出即可;
(3)根据W=y1+y2,分别根据二次函数最值求法以及t的取值范围求出即可.
解答:解:(1)当0≤t≤1.5时,设y1=at,则45=1.5a,
解得:a=30,
∴y1=30t,
当1.5≤t时,设y1=bt+c,则
,
解得:
∴y1=20t+15,
故y1=
;
(2)当0≤t≤1时,由图象可得出,抛物线顶点坐标为(1,90),且过点(0,0),
设y2=a(t-1)2+90,
将(0,0)代入得出:a=-90,
∴y2=-90(t-1)2+90=-90t2+180t,
当1≤t时,设y2=kt+d,则
,
解得:
,
∴y2=10t+80,
故y2=
;
(3)设用于数学学习的时间为t,根据题意得:
①当0≤t≤0.5时:w=20(2-t)+15-90t2+180t=-90(t-
)2+126
,当t=0.5时,w最大=112.5,
②当0.5≤t≤1时:w=30(2-t)+-90t2+180t=-90(t-
)2+122.5,当t=
时,w最大=122.5,
③当1≤t≤2时:w=30(2-t)+10t+80=-20t+140,当t=1时,w最大=120.
综上所得,应安排
小时用于数学学习,
小时用于非数学学科的学习,才能使学习的总收益量最大.
解得:a=30,
∴y1=30t,
当1.5≤t时,设y1=bt+c,则
|
解得:
|
∴y1=20t+15,
故y1=
|
(2)当0≤t≤1时,由图象可得出,抛物线顶点坐标为(1,90),且过点(0,0),
设y2=a(t-1)2+90,
将(0,0)代入得出:a=-90,
∴y2=-90(t-1)2+90=-90t2+180t,
当1≤t时,设y2=kt+d,则
|
解得:
|
∴y2=10t+80,
故y2=
|
(3)设用于数学学习的时间为t,根据题意得:
①当0≤t≤0.5时:w=20(2-t)+15-90t2+180t=-90(t-
| 8 |
| 9 |
| 1 |
| 9 |
②当0.5≤t≤1时:w=30(2-t)+-90t2+180t=-90(t-
| 5 |
| 6 |
| 5 |
| 6 |
③当1≤t≤2时:w=30(2-t)+10t+80=-20t+140,当t=1时,w最大=120.
综上所得,应安排
| 5 |
| 6 |
| 7 |
| 6 |
点评:此题主要考查了函数定义、性质以及在实际问题中的应用等,利用自变量的取值范围进行分段讨论得出是解题关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
为极大地满足人民生活的需求,丰富市场供应,我市农村温棚设施技术迅速发展,温棚种植面积不断扩大,在耕地上培成一行一行的矩形土埂,按顺序间隔种植不同农耕作物的方法叫分垄间隔套种,科学研究表明:在塑料温棚中分垄间隔套种高矮不同的蔬菜和水果,可增加它们的光合作用,提高单位面积的产量和经济效益.
现有一种植总面积为5亩的矩形塑料温棚,分垄间隔套种花生和草莓,经实验研究表明,花生的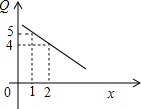 每亩产量P(千克/亩)与亩数x(亩)之间关系如下表格,草莓每亩产量Q(千克/亩)与亩数x间关系如下函数图象.
每亩产量P(千克/亩)与亩数x(亩)之间关系如下表格,草莓每亩产量Q(千克/亩)与亩数x间关系如下函数图象.
(1)现规定花生与草莓的亩数都不少于1,求P与x及Q与x函数关系式,并求自变量x的取值范围;
(2)如果种植花生m亩,应如何安排种植面积,使总产量最大,并求总产量的最大值;
(3)经市场调查发现,每千克花生售价为2元,每千克草莓售价为5元,如何调整种植面积,使销售额等于100元(
≈3.6).
现有一种植总面积为5亩的矩形塑料温棚,分垄间隔套种花生和草莓,经实验研究表明,花生的
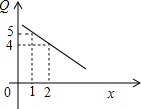 每亩产量P(千克/亩)与亩数x(亩)之间关系如下表格,草莓每亩产量Q(千克/亩)与亩数x间关系如下函数图象.
每亩产量P(千克/亩)与亩数x(亩)之间关系如下表格,草莓每亩产量Q(千克/亩)与亩数x间关系如下函数图象.
| x(亩) | 1 | 2 | 3 | 4 | 5 |
| P(千克/亩) | 12 | 14 | 16 | 18 | 20 |
(2)如果种植花生m亩,应如何安排种植面积,使总产量最大,并求总产量的最大值;
(3)经市场调查发现,每千克花生售价为2元,每千克草莓售价为5元,如何调整种植面积,使销售额等于100元(
| 13 |
为极大地满足人民生活的需求,丰富市场供应,我市农村温棚设施技术迅速发展,温棚种植面积不断扩大,在耕地上培成一行一行的矩形土埂,按顺序间隔种植不同农耕作物的方法叫分垄间隔套种,科学研究表明:在塑料温棚中分垄间隔套种高矮不同的蔬菜和水果,可增加它们的光合作用,提高单位面积的产量和经济效益.
现有一种植总面积为5亩的矩形塑料温棚,分垄间隔套种花生和草莓,经实验研究表明,花生的 每亩产量P(千克/亩)与亩数x(亩)之间关系如下表格,草莓每亩产量Q(千克/亩)与亩数x间关系如下函数图象.
每亩产量P(千克/亩)与亩数x(亩)之间关系如下表格,草莓每亩产量Q(千克/亩)与亩数x间关系如下函数图象.
| x(亩) | 1 | 2 | 3 | 4 | 5 |
| P(千克/亩) | 12 | 14 | 16 | 18 | 20 |
(2)如果种植花生m亩,应如何安排种植面积,使总产量最大,并求总产量的最大值;
(3)经市场调查发现,每千克花生售价为2元,每千克草莓售价为5元,如何调整种植面积,使销售额等于100元(
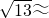 3.6).
3.6).