题目内容
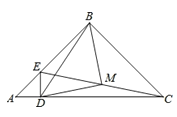
【题目】(![]() )如图
)如图![]() 中,
中,![]() ,请用直尺和圆规作一条直线,把
,请用直尺和圆规作一条直线,把![]() 分割成两个等腰三角形(不写作法,但须保留作图痕迹).
分割成两个等腰三角形(不写作法,但须保留作图痕迹).
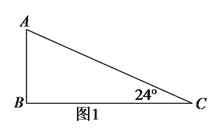
(![]() )如图
)如图![]() 中,
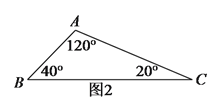
中,![]() 的三个内角分别为
的三个内角分别为![]() ,
,![]() ,
,![]() ,若
,若![]() ,
,![]() ,
,![]() ,在
,在![]() 上找一个点
上找一个点![]() ,使
,使![]() 为等腰三角形,求出
为等腰三角形,求出![]() 的长(可用含
的长(可用含![]() 的代数式表示).
的代数式表示).


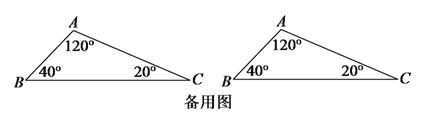
【答案】(1)图形见解析;(2)![]() 的长为
的长为![]() 或
或![]() 或
或![]() .
.
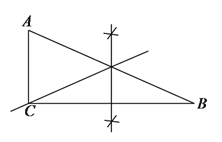
【解析】试题分析:(1)尺规作图,作出BC的垂直平分线,将点C和中垂线与线段AB的交点连接起来即可;(2)要使△ABP为等腰三角形,由于没有明确指出腰和底,因此要分类讨论,分三类:①BP=BA,②AP=AB,③PA=PB,分别求出三种情况下BP的长即可.
试题解析:
(![]() )如图所示:直线
)如图所示:直线![]() 即为所求,
即为所求,
(![]() )①当BP=BA时,BP=4;
)①当BP=BA时,BP=4;

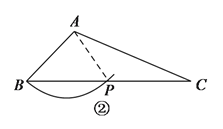
②当AP=AB时,∠APB=∠B=40°,
∴∠PAC=∠C=20°,
∴PA=PC=4,
∴BP=a-4;
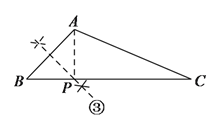
③当PA=PB时,∠BAP=∠B=40°,
∴∠CAP=∠CPA=80°,
∴CP=CA=6,
∴BP=a-6.
∴BP的长为4或a-4或a-6.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目