��Ŀ����
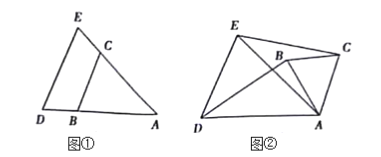
����Ŀ����ͼ�٣��ڡ�ABC���ADE�У�AB=AC��AD=AE����A�ǹ����ǡ�
��1��BD��CE��������ϵ�ǣ�BD______CE��
��2����ͼ�١�ABC�Ƶ�A��תһ���ĽǶȣ��õ���ͼ����ʾ��ͼ�Ρ�
����֤��BD��CE��
��BD��CE����ֱ�ߵļн����DAE��������ϵ��ʲô��˵�����ɡ�
��3����AD=10��AB=6����ͼ���еġ�ABC�Ƶ�A˳ʱ����ת����(0��<����360)ֱ��д��BD���ȵ�ȡֵ��Χ��
���𰸡���1��=����2������������3��4��BD��16.
�������������������1�����߶εĺͲ�ɵõ�������
��2��������ת�����ʵõ���DAE=��BAC�������õ���BAD=��CAE��Ȼ��֤����ABD����ACE������ȫ�������εĶ�Ӧ����ȼ��ɵõ����ۣ�
���ӳ�DB��CE�ڵ�F����ȫ�������ζ�Ӧ����ȣ��õ���ADB=��AEC�������������ڽǺͶ������ɵõ����ۣ�
����B���߶�DA��ʱ��DB�������B��DA���ӳ�����ʱ��DB����ɴ˼��ɵó����ۣ�
����������⣺��1��=���������£�
��AB=AC��AD=AE����AD- AB =AE �CAC����BD��CE��
��2��������ת�����ʵõ�����DAE=��BAC�����DAE+��BAE=��BAC+��BAE������BAD=��CAE������ABD�͡�ACE�У���AB=AC����BAD=��CAE��AD=AE������ABD����ACE��SAS������BD=CE��
��BD��CE����ֱ�ߵļн����DAE�Ķ�����ȣ��ӳ�DB��CE�ڵ�F��

����ABD����ACE�����ADB=��AEC��
�֡ߡ�AOD=��EOF����180��-��ADB-��AOD =180��-��AEC-��EOF������DAE=��DFE��
����B���߶�DA��ʱ��DB=DA-BA=4�������B��DA���ӳ�����ʱ��DB=DA+BA=16�����4��BD��16��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�