Question

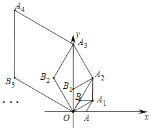
【题目】如图，在平面直角坐标系中，OA＝1，以OA为一边，在第一象限作菱形OAA1B，并使∠AOB＝60°，再以对角线OA1为一边，在如图所示的一侧作相同形状的菱形OA1A2B1，再依次作菱形OA2A3B2，OA3A4B3，……，则过点B2018，B2019，A2019的圆的圆心坐标为_____．

Answer 1

【答案】（-（）2018，（）2019）

【解析】

过A1作A1C⊥x轴于C，由菱形的性质得到OA＝AA1＝1，∠A1AC＝∠AOB＝60°，根据勾股定理得到OA1＝，求得∠A2B1A3＝60°，解直角三角形得到B1A3＝2，A2A3＝3，求得OA3＝OB1+B1A3＝3＝（）3得到菱形OA2A3B2的边长＝3＝（）2，设B1A3的中点为O1，连接O1A2，O1B2，推出过点B1，B2，A2的圆的圆心坐标为O1（0，2），以此类推，于是得到结论．

解：过A1作A1C⊥x轴于C，

∵四边形OAA1B是菱形，

∴OA＝AA1＝1，∠A1AC＝∠AOB＝60°，

∴A1C＝，AC＝，

∴OC＝OA+AC＝，

在Rt△OA1C中，OA1＝，

∵∠OA2C＝∠B1A2O＝30°，∠A3A2O＝120°，

∴∠A3A2B1＝90°，

∴∠A2B1A3＝60°，

∴B1A3＝2，A2A3＝3，

∴OA3＝OB1+B1A3＝3＝（）3

∴菱形OA2A3B2的边长＝3＝（）2，

设B1A3的中点为O1，连接O1A2，O1B2，

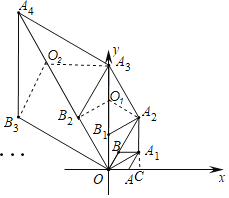
于是求得，O1A2＝O1B2＝O1B1＝＝（）1，

∴过点B1，B2，A2的圆的圆心坐标为O1（0，），

∵菱形OA3A4B3的边长为3＝（）3，

∴OA4＝9＝（）4，

设B2A4的中点为O2，

连接O2A3，O2B3，

同理可得，O2A3＝O2B3＝O2B2＝3＝（）2，

∴过点B2，B3，A3的圆的圆心坐标为O2（﹣3，3），…以此类推，菱形OA2019A2020B2019的边长为（）2019，

OA2020＝（）2020，

设B2018A2020的中点为O2018，连接O2018A2019，O2018B2019，

求得，O2018A2019＝O2018B2019＝O2018B2018＝（）2018，

∴点O2018是过点B2018，B2019，A2019的圆的圆心，

∵2018÷12＝168…2，

∴点O2018在射线OB2上，

则点O2018的坐标为（﹣（）2018，（）2019），

即过点B2018，B2019，A2019的圆的圆心坐标为：（﹣（）2018，（）2019），

故答案为：（﹣（）2018，（）2019）．