Question

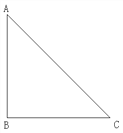
【题目】如图，已知，在Rt ΔABC中，∠ABC=900, AB＝BC＝2.

（1）用尺规作∠A的平分线AD.

（2）角平分线AD交BC于点D,求BD的长.

Answer 1

【答案】（1）见解析（2）2﹣2

【解析】试题分析：（1）利用基本作作（作已知角的平分线）作AD平分∠BAC；

（2）作DE⊥AC于E，如图，先判断△ABC为等腰直角三角形得到∠C=45°，则可判断△CDE为等腰直角三角形，则CD=DE，再根据角平分线的性质得到BD=BE，设BD=x，则CD=x，然后利用BC=2列方程x+x=2，再解方程即可．

解：（1）如图，AD为所求；

（2）作DE⊥AC于E，如图，

∵∠ABC=90°，AB=BC=2．

∴△ABC为等腰直角三角形，

∴∠C=45°，

∴△CDE为等腰直角三角形，

∴CD=DE，

∵AD为角平分线，DB⊥AB，DE⊥AC，

∴BD=BE，

设BD=x，则CD=x，

∴x+x=2，

∴x=2（﹣1）=2﹣2，

即BD的长为2﹣2．