Question

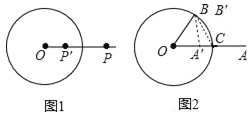
【题目】如图1，⊙O的半径为r（r＞0），若点P′在射线OP上，满足OP′OP=r2，则称点P′是点P关于⊙O的“反演点”．

如图2，⊙O的半径为4，点B在⊙O上，∠BOA=60°，OA=8，若点A′，B′分别是点A，B关于⊙O的反演点，求A′B′的长．

Answer 1

【答案】2．

【解析】

试题分析：设OA交⊙O于C，连结B′C，如图2，根据新定义计算出OA′=2，OB′=4，则点A′为OC的中点，点B和B′重合，再证明△OBC为等边三角形，则B′A′⊥OC，然后在Rt△OA′B′中，利用正弦的定义可求A′B′的长．

试题解析：设OA交⊙O于C，连结B′C，如图2，

∵OA′OA=42，

而r=4，OA=8，

∴OA′=2，

∵OB′OB=42，

∴OB′=4，即点B和B′重合，

∵∠BOA=60°，OB=OC，

∴△OBC为等边三角形，

而点A′为OC的中点，

∴B′A′⊥OC，

在Rt△OA′B′中，sin∠A′OB′=，

∴A′B′=4sin60°=2．