��Ŀ����
����Ŀ���Ҹ������ƽ�������彨���У����������Ҹ��㳡���ƻ�������ͬ��С�����ĺ�ɫ����ɫ��ש���������飬��ȡ��Ϣ���±���
��� | ������������500�� | ��������������500�� |
��ɫ��ש | ԭ������ | �������� |
��ɫ��ש | ԭ������ | �Ծ������� |
�������ɫ��ש400�飬��ɫ��ש600�飬�踶��8600Ԫ���������ɫ��ש1000�飬��ɫ��ש350�飬�踶��9900Ԫ��
��1����ɫ��ש����ɫ��ש�ĵ��۸�����Ԫ��
��2���������㣬��Ҫ���õ�ש1200�飬������ɫ��ש�����������ں�ɫ��ש��һ�룬���Ҳ�����600�飬��ι������٣������Ƕ���Ԫ����˵�����ɣ�
���𰸡���1����ɫ��שÿ��8Ԫ����ɫ��שÿ��10Ԫ����2��������ɫ��ש700�飬��ɫ��ש500�飬�������٣����ٷ���Ϊ8980Ԫ��
��������
��1�����������ϱ��������ݣ������ɫ��ש4000�飬��ɫ��ש6000�飬�踶��86000Ԫ�������ɫ��ש10000�飬��ɫ��ש3500�飬�踶��99000Ԫ���ֱ�ó����̵ó��𰸣�
��2��������֪�ó�x��ȡֵ��Χ��������һ�κ��������Եó��𰸣�
��1�����ɫ��שÿ��xԪ����ɫ��שÿ��yԪ��������ɵã�
![]() ��
��
���![]() ��
��
�𣺺�ɫ��שÿ��8Ԫ����ɫ��שÿ��10Ԫ��
��2���蹺����ɫ��שa�飬���ú�ɫ��ש��1200��a���飬������ܷ���ΪyԪ��
������ɵã�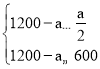 ��
��
��ã�600��a��800��
��600��a��700ʱ��
y��8a��0.8+0.9��10��1200��a����10800��2.6a��
��a��700ʱy����СֵΪ��10800��2.6��700��8980��
��700��x��800ʱ��y��8a��0.8+10��1200��a������3.6a+12000��
��a��800ʱ��y����СֵΪ����3.6��800+12000��9120��
��9120��9180��
�����ɫ��ש700�飬��ɫ��ש500�飬�������٣����ٷ���Ϊ8980Ԫ��

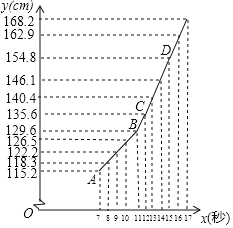
����Ŀ����ѧ��ȤС��Ϊ���о���Сѧ��������y��cm��������x���꣩�Ĺ�ϵ����ij�й����ϵõ��˸���2017��ͳ�Ƶ���Сѧ�������������ƽ�����ߣ����±�����ͼ�Ѿ���ֱ������ϵ������˱������ݶ�Ӧ�ĵ㣬������ǰ5�������λ��ֱ��AB�ϣ���7�������λ��ֱ��CD�ϣ�
������x | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
����ƽ������y | 115.2 | 118.3 | 122.2 | 126.5 | 129.6 | 135.6 | 140.4 | 146.1 | 154.8 | 162.9 | 168.2 |
��1��������ѧ����ƽ�����ߴ��� ���꿪ʼ�����ر�Ѹ�٣�
��2����ֱ��AB����Ӧ�ĺ�������ʽ��
��3��ֱ��д��ֱ��CD����Ӧ�ĺ�������ʽ������17�������������������ٶȴ��·���ֱ��CD����Ӧ�ĺ�����ϵ������Ԥ�����18�������������ƽ�����ߴ�Լ�Ƕ��٣�