题目内容
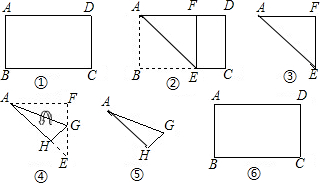
矩形纸片ABCD中，AD=4cm，AB=10cm，按如图所示的方式折叠使点B和点D重合，折痕为EF，且AD2+AE2=DE2，则DE的长为（ ）分析：根据翻折的性质可得DE=BE，然后用DE表示出AE，再代入等式进行计算即可得解．
解答：解：∵矩形纸片ABCD折叠后点B和点D重合，
∴DE=BE，
∴AE=AB-BE=AB-DE=10-DE，
∵AD2+AE2=DE2，
∴42+（10-DE）2=DE2，
解得DE=
cm．
故选D．
∴DE=BE，
∴AE=AB-BE=AB-DE=10-DE，
∵AD2+AE2=DE2，
∴42+（10-DE）2=DE2，
解得DE=
| 29 |
| 5 |
故选D．
点评：本题考查了翻折变换的性质，是基础题，熟记翻折前后的两个图形能够完全重合得到DE=BE是解题的关键．
练习册系列答案
期末集结号系列答案
相关题目
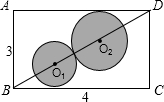如图，矩形纸片ABCD中，AB=3cm，BC=4cm，若要在该纸片中剪下两个外切的圆⊙O1和⊙O2，要求⊙O1和⊙O2的圆心均在对角线BD上，且⊙O1和⊙O2分别与BC、AD相切，则O1O2的长为（ ）
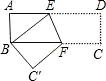如图，矩形纸片ABCD中，AD=9，AB=3，将其折叠，使点D与点B重合，折痕为EF，那么折痕EF的长为
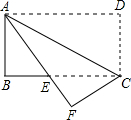如图，在矩形纸片ABCD中，将矩形纸片沿着对角线AC折叠，使点D落在点F处，设AF与BC相交于点E．
