题目内容
关于x的一元二次方程x2+mx+9=0有两个相等的实数根,则m的值是( ▲ )
| A.3或-3 | B.6 | C.-6 | D.6或-6 |
D
分析:由方程有两个相等的实数根,得到根的判别式等于0,列出关于m的方程,求出方程的解即可得到m的值.
解答:解:∵方程x2+mx+9=0有两个相等的实数根,
∴b2-4ac=0,即m2-36=0,
解得:m=±6.
故选D
点评:此题考查了根判别式的应用,一元二次方程根的判别式决定了方程解的情况:当b2-4ac>0,方程有两个不相等的实数根;当b2-4ac=0时,方程有两个相等的实数根;当b2-4ac<0时,方程没有实数根.熟练掌握此性质是解本题的关键.
解答:解:∵方程x2+mx+9=0有两个相等的实数根,
∴b2-4ac=0,即m2-36=0,
解得:m=±6.
故选D
点评:此题考查了根判别式的应用,一元二次方程根的判别式决定了方程解的情况:当b2-4ac>0,方程有两个不相等的实数根;当b2-4ac=0时,方程有两个相等的实数根;当b2-4ac<0时,方程没有实数根.熟练掌握此性质是解本题的关键.

练习册系列答案
相关题目
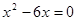 小题2:
小题2: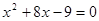
 的根是
的根是  =x的解是 ( )
=x的解是 ( )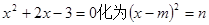 的形式,指出
的形式,指出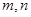 分别是(▲).
分别是(▲).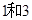

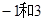

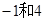
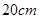 ,长
,长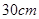 的图案,其中有两横两竖的彩条,横竖彩条的宽度比是
的图案,其中有两横两竖的彩条,横竖彩条的宽度比是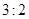 ,如果要使彩条所占的面积是图案的面积的三分之一,应如何设计彩条的宽度?
,如果要使彩条所占的面积是图案的面积的三分之一,应如何设计彩条的宽度?
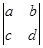 的意义是
的意义是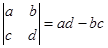 ,则当
,则当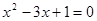 时,
时, 。
。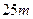 的墙,用
的墙,用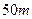 长的篱笆,围成一个长方形的养鸡场.
长的篱笆,围成一个长方形的养鸡场.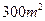 的长方形养鸡场?
的长方形养鸡场?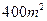 的长方形养鸡场?如能,说明围法;如不能,请说明理由.
的长方形养鸡场?如能,说明围法;如不能,请说明理由.
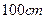 ,宽
,宽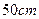 ,在他的四角各切去一个同样的正方形,然后将四周突出部分折起,就能制作一个无盖方盒。如果要制作的无盖方盒的底面积为
,在他的四角各切去一个同样的正方形,然后将四周突出部分折起,就能制作一个无盖方盒。如果要制作的无盖方盒的底面积为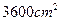 ,那么铁皮各角应切去边长为多大的正方形?
,那么铁皮各角应切去边长为多大的正方形?