题目内容
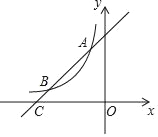
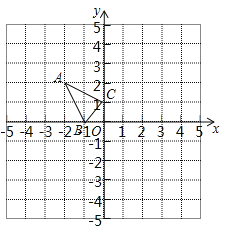
【题目】如图1，在平面直角坐标系中，直线y＝﹣5x+5与x轴，y轴分别交于A，C两点，抛物线y＝x2+bx+c经过A，C两点，与x轴的另一交点为B．
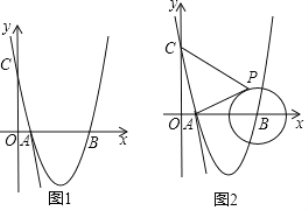
（1）求抛物线解析式及B点坐标；
（2）若点M为x轴下方抛物线上一动点，连接MA、MB、BC，当点M运动到某一位置时，四边形AMBC面积最大，求此时点M的坐标及四边形AMBC的面积；
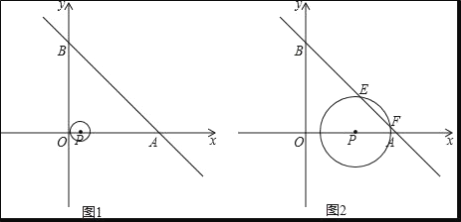
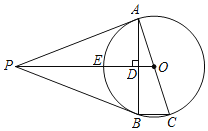
（3）如图2，若P点是半径为2的⊙B上一动点，连接PC、PA，当点P运动到某一位置时，PC+
PA的值最小，请求出这个最小值，并说明理由．
【答案】（1）y＝x2﹣6x+5， B（5，0）；（2）当M（3，﹣4）时，四边形AMBC面积最大，最大面积等于18；（3）PC+
PA的最小值为
，理由详见解析.
【解析】
（1）由直线y＝﹣5x+5求点A、C坐标，用待定系数法求抛物线解析式，进而求得点B坐标．
（2）从x轴把四边形AMBC分成△ABC与△ABM；由点A、B、C坐标求△ABC面积；设点M横坐标为m，过点M作x轴的垂线段MH，则能用m表示MH的长，进而求△ABM的面积，得到△ABM面积与m的二次函数关系式，且对应的a值小于0，配方即求得m为何值时取得最大值，进而求点M坐标和四边形AMBC的面积最大值．
（3）作点D坐标为（4，0），可得BD＝1，进而有
，再加上公共角∠PBD＝∠ABP，根据两边对应成比例且夹角相等可证△PBD∽△ABP，得
等于相似比，进而得PD＝AP，所以当C、P、D在同一直线上时，PC+PA＝PC+PD＝CD最小．用两点间距离公式即求得CD的长．
解：（1）直线y＝﹣5x+5，x＝0时，y＝5
∴C（0，5）
y＝﹣5x+5＝0时，解得：x＝1
∴A（1，0）
∵抛物线y＝x2+bx+c经过A，C两点
∴
解得：
∴抛物线解析式为y＝x2﹣6x+5
当y＝x2﹣6x+5＝0时，解得：x1＝1，x2＝5
∴B（5，0）
（2）如图1，过点M作MH⊥x轴于点H
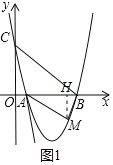
∵A（1，0），B（5，0），C（0，5）
∴AB＝5﹣1＝4，OC＝5
∴S△ABC＝ABOC＝×4×5＝10
∵点M为x轴下方抛物线上的点
∴设M（m，m2﹣6m+5）（1＜m＜5）
∴MH＝|m2﹣6m+5|＝﹣m2+6m﹣5
∴S△ABM＝ABMH＝×4（﹣m2+6m﹣5）＝﹣2m2+12m﹣10＝﹣2（m﹣3）2+8
∴S四边形AMBC＝S△ABC+S△ABM＝10+[﹣2（m﹣3）2+8]＝﹣2（m﹣3）2+18
∴当m＝3，即M（3，﹣4）时，四边形AMBC面积最大，最大面积等于18
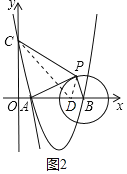
（3）如图2，在x轴上取点D（4，0），连接PD、CD
∴BD＝5﹣4＝1
∵AB＝4，BP＝2
∴
∵∠PBD＝∠ABP
∴△PBD∽△ABP
∴
∴PD＝AP
∴PC+PA＝PC+PD
∴当点C、P、D在同一直线上时，PC+PA＝PC+PD＝CD最小
∵CD＝
∴PC+PA的最小值为
