题目内容
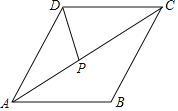
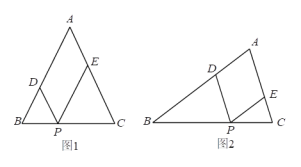
【题目】如图1，△ABC为等腰三角形，AB=AC=a，P点是底边BC上的一个动点，PD∥AC，PE∥AB．
⑴用a表示四边形ADPE的周长为 ；
⑵点P运动到什么位置时，四边形ADPE是菱形，请说明理由；
⑶如果△ABC不是等腰三角形(图2)，其他条件不变，点P运动到什么位置时，四边形ADPE是菱形(不必说明理由)．
【答案】⑴2a；⑵见解析;(3)见解析.
【解析】
（1）由题意可得四边形ADPE为平行四边形，由平行线的性质和等腰三角形的性质可得DB=DP，即可求四边形ADPE的周长；
（2）当P为BC中点时，四边形ADPE是菱形，由等腰三角形的性质和平行线的性质可得AE=EP，则平行四边形ADPE是菱形；
（3）P运动到∠A的平分线上时，四边形ADPE是菱形，首先证明四边形ADPE是平行四边形，再根据平行线的性质可得∠1=∠3，从而可证出∠2=∠3，进而可得AE=EP，然后可得四边形ADPE是菱形．
解：⑴∵PD∥AC，PE∥AB，
∴四边形ADPE为平行四边形，
∴AD=PE，DP=AE，
∵AB=AC，
∴∠B=∠C，
∵DP∥AC，
∴∠B=∠DPB，
∴DB=DP，
∴四边形ADPE的周长=2(AD+DP)=2(AD+BD)=2AB=2a；
故答案为：2a；
⑵当P为BC中点时，四边形ADPE是菱形．
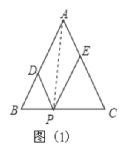
理由如下：连结AP，
∵PD∥AC，PE∥AB，
∴四边形ADPE为平行四边形，
∵AB=AC，P为BC中点，
∴∠PAD=∠PAE，
∵PE∥AB，
∴∠PAD=∠APE，
∴∠PAE=∠APE，
∴EA=EP，
∴四边形ADPE是菱形；
⑶P运动到∠A的平分线上时，四边形ADPE是菱形，
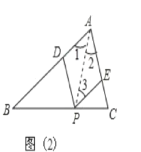
∵PD∥AC，PE∥AB，
∴四边形ADPE是平行四边形，
∵AP平分∠BAC，
∴∠1=∠2，
∵AB∥EP，
∴∠1=∠3，
∴∠2=∠3，
∴AE=EP，
∴四边形ADPE是菱形．
