题目内容
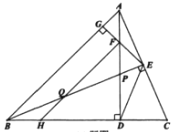
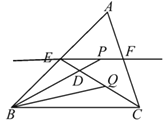
【题目】如图所示,在△ABC中,BC=4,E,F分别是AB,AC的中点,动点P在直线EF上,∠CBP的平分线交CE于点Q,当点Q把线段EC分成的两线段之比是1:2时,线段EP、BP满足的数量关系是__________________________.
【答案】![]() 或
或![]() .
.
【解析】
根据题意,点Q把线段EC分成的两线段之比是1:2时,则可以分为两类进行讨论:①![]() ,②
,②![]() ;利用相似三角形的判定和性质,以及等腰三角形的性质,即可得到答案.
;利用相似三角形的判定和性质,以及等腰三角形的性质,即可得到答案.
解:根据题意,∵E,F分别是AB,AC的中点,
∴EF是△ABC的中位线,
∴EF∥BC,
∴△EGQ∽△CBQ,∠PGB=∠CBG,
∴![]() .
.
∵BQ平分∠CBP,
∴∠PBG=∠CBG,
∴∠PGB=∠PBG,
∴BP=PG,
∵GE=EP+PG,
∴GE=EP+BP.
∵点Q把线段EC分成的两线段之比是1:2,
∴![]() 或
或![]() ;
;
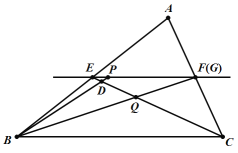
①当![]() 时,如图:
时,如图:
 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
②当![]() 时,如图:
时,如图:
 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
∴故答案为:![]() 或
或![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目