题目内容
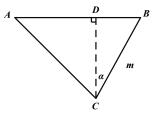
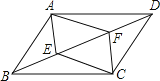
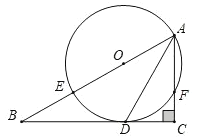
【题目】如图，在
中，
，两条高AD，BE交于点P.过点E作
，垂足为G，交AD于点F，过点F作
，交BC于点H，交BE交于点Q，连接DE.
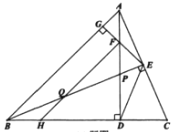
（1）若
，
，求DE的长
（2）若
，求证：
.
【答案】（1）
；（2）详见解析.
【解析】
（1）首先证明AE=CE，在Rt△ADC中，根据勾股定理求出AC的长，再运用直角三角形斜边上的中线的性质计算即可；
（2）连接DQ，根据等腰三角形的性质得
，进而证明
和
是等腰直角三角形，再证明
和
得
，故可证
为等腰直角三角形，
，结合（1）的结论易证得
．
（1）∵
，BE是高，
∴
∵AD是
的高，
∴
在
中，
.
∴
.
∴
（2）连接DQ
∵
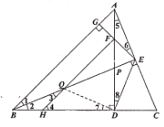
，BE是AC边上的高，
，
∴BE平分
，
，
∴
∵
，∴
，
∵AD是BC边上的高，
∴
∴和是等腰直角三角形.
∴
，
.∴
∵
，
，，
∴
，
，
∴
.
∵
，
，，
∴（AAS）
∴
又∵，，
∴（SAS）
∴，
∵
，∴
，即
∴为等腰直角三角形
∴
由（1）已证
∴
，
∵
，
∴
练习册系列答案
相关题目
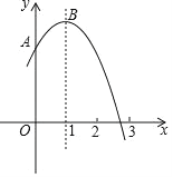
【题目】二次函数
为常数，
中的
与
的部分对应值如下表：
x | -1 | 0 | 3 |
y | n | -3 | -3 |
当
时，下列结论中一定正确的是________(填序号即可)
①
；②当
时，的值随值的增大而增大；③
；④当
时，关于的一元二次方程
的解是
，
．
