Question

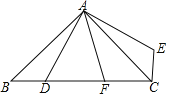
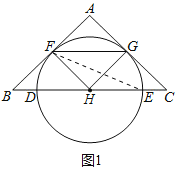
【题目】如图，在△ABC中，AB＝AC，BC是经过⊙H的圆心，交⊙H于点D、E，AB、AC是圆的切线，F、G是切点．

（1）求证：BH＝CH；

（2）填空：①当∠FHG＝　 　时，四边形FHCG是平行四边形；

②当∠FED＝　 　时，四边形AFHG是正方形．

Answer 1

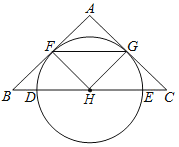
【答案】（1）见解析；（2）①90°；②22.5°

【解析】

（1）证明△BFH≌△CGH可得结论．

（2）①当∠FHG＝90°时，四边形FHCG是平行四边形．分别证明FG∥CH，FH∥CG即可．

②当∠FED＝22.5°时，四边形AFHG是正方形．连接EF，首先证明∠AFH＝∠FHG＝∠AGH＝90°，推出四边形AFHG是矩形，再根据HF＝HG推出四边形AFHG是正方形．

（1）证明：∵AB＝AC，

∴∠B＝∠C．

∵AB、AC是⊙H的切线，

∴∠BFH＝∠CGH＝90°．

∵HF＝HG，

∴△BFH≌△CGH（AAS），

∴BH＝CH．

（2）解：①当∠FHG＝90°时，四边形FHCG是平行四边形．

理由：∵△BFH≌△CGH（已证），

∴BF＝CG，

∵AB＝AC，

∴AF＝AG，

∴∠AFG＝∠AGF，

∵∠B＝∠C，∠A+2∠AGF＝180°，∠A+2∠C＝180°，

∴∠AGF＝∠C，

∴，

∵AC是⊙H的切线，

∴AC⊥HG，

∴∠FHG＝∠CGH＝90°，

∴，

∴四边形FHCG是平行四边形．

②当∠FE D＝22.5°时，四边形AFHG是正方形．

理由：如图1中，连接EF．

，

，

∴∠FHD＝2∠FED＝45°，

∵△BFH≌△CGH（已证），

∴∠FHB＝∠GHC＝45°，

∴∠FHG＝90°，

∵AB，AC是⊙H的切线，

∴AB⊥HF，AC⊥HG，

∴∠AFH＝∠AGH＝90°，

∴四边形AFHG是矩形，

∵HF＝HG，

∴四边形AFHG是正方形．