题目内容
【题目】点E为射线BC上一点,∠B+∠DCB=180°,连接ED,过点A的直线MN∥ED. 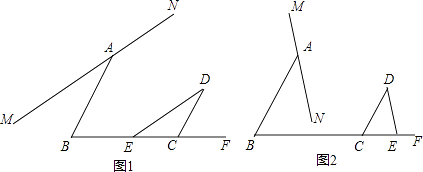
(1)如图1,当点E在线段BC上时,猜想并验证∠MAB=∠CDE.
(2)如图2,当点E在线段BC的延长线时,猜想并验证∠MAB与∠CDE的数量关系.
【答案】
(1)猜想:∠MAB=∠D,
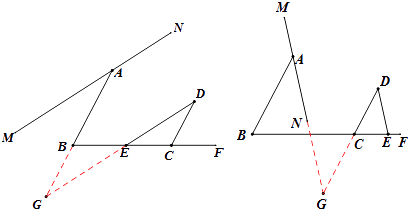
证明:延长AB、DE交于点G,
∵∠B+∠DCB=180°,
∴AB∥DC,
∴∠D=∠G,
∵MN∥ED,
∴∠MAB=∠G,
∴∠MAB=∠D;
(2)猜想:∠MAB+∠CDE=180°.
证明:延长AN、DC 交于点G,
∵∠B+∠DCB=180°,
∴AB∥DC,
∴∠D=∠G,
∵MN∥ED,
∴∠NAB=∠G,
∴∠NAB=∠D,
∵∠NAB+∠MAB=180°,
∴∠D+∠MAB=180°.
【解析】(1)延长AB、DE交于点G,根据平行线的判定定理得到AB∥DC,由平行线的性质得到∠D=∠G,∠MAB=∠G,等量代换即可得到结论;(2)延长AN、DC 交于点G,根据平行线的判定定理得到AB∥DC,由平行线的性质得到∠D=∠G,∠NAB=∠G,等量代换得到∠NAB=∠D,于是得到结论.
【考点精析】本题主要考查了平行线的判定与性质的相关知识点,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能正确解答此题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目