题目内容
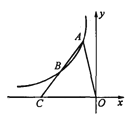
【题目】如图，A、B是第二象限内双曲线y＝
上的点，A、B两点的横坐标分别是a、2a，线段AB的延长线交x轴于点C，若S△AOC＝6，则k的值为 ．
【答案】-4.
【解析】
试题分析：分别过点A、B作AF⊥y轴于点F，AD⊥x轴于点D，BG⊥y轴于点G，BE⊥x轴于点E，由于反比例函数的图象在第二象限，所以k＜0，由点A是反比例函数图象上的点可知，S△AOD=S△AOF=
，再由A、B两点的横坐标分别是a、2a可知AD=2BE，故点B是AC的二等分点，故DE=a，CE=a，所以S△AOC=S梯形ACOF-S△AOF=6，故可得出k的值．
试题解析：分别过点A、B作AF⊥y轴于点F，AD⊥x轴于点D，BG⊥y轴于点G，BE⊥x轴于点E，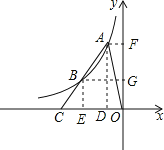
∵反比例函数y=
的图象在第二象限，
∴k＜0，
∵点A是反比例函数图象上的点，
∴S△AOD=S△AOF=，
∵A、B两点的横坐标分别是a、2a，
∴AD=2BE，
∴点B是AC的二等分点，
∴DE=a，CE=a，
∴S△AOC=S梯形ACOF-S△AOF=
（OE+CE+AF）×OF-=×4a×
-=6，
解得k=-4.
练习册系列答案
相关题目
【题目】一支原长为20cm的蜡烛，点燃后，其剩余长度y（cm）与燃烧时间x（min）之前的关系如表：
燃烧时间x（min） | 10 | 20 | 30 | 40 | 50 | … |
剩余长度y（cm） | 19 | 18 | 17 | 16 | 15 | … |
（1）表中反映的自变量是什么？因变量是什么？
（2）求出剩余长度y（cm）与燃烧时间x（min）之间的关系式；
（3）估计这支蜡烛最多可燃烧多少分钟？
