题目内容
【题目】如图1,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.
(1)将图1中的三角板OMN绕点O按逆时针方向旋转,使∠BON=30°,如图2,MN与CD相交于点E,求∠CEN的度数;
(2)将图1中的三角尺OMN绕点O按每秒20°的速度沿逆时针方向旋转一周,在旋转的过程中,求在第几秒时,边MN恰好与边CD平行?(友情提醒:先画出符合题意的图形,然后再探究)
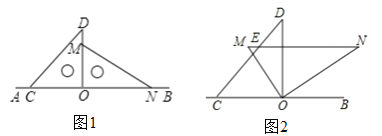
【答案】( (1)∠CEN=135°;(2)3.75秒或12.75秒.
【解析】
(1)根据内错角相等,两直线平行判断出MN∥BC,再根据两直线平行,同旁内角互补解答;
(2)作出图形,然后分两种情况求出旋转角,再根据时间=旋转角÷速度计算即可得解.
(1)∵∠BON=∠N=30°,
∴MN∥BC,
∴∠CEN=180°-∠DCO=180°-45°=135°;
(2)如图,MN∥CD时,旋转角为90°-(60°-45°)=75°,
或270°-(60°-45°)=255°,
所以,t=75°÷20°=3.75秒,
或225°÷20°=12.75秒

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目