Question

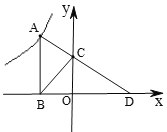
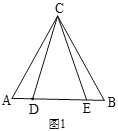
【题目】基础探究：如图1，在,中，，，点、都在边上，且，连接、．

（1）求证：．

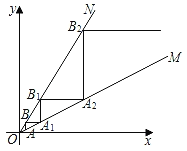
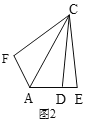
（2）如图2，以为对角线的四边形中，，，将沿折叠，得到，点的对应点恰好落在边上，若，，则四边形的面积为________．

Answer 1

【答案】（1）见解析；（2）．

【解析】

（1）由AC=AB，∠CAB=60°可证明△ABC是等边三角形，可得∠A=∠B=60°，CA=CB，利用SAS可证明△CAD≌△CBE，可得CD=CE，根据等腰三角形的性质即可得出∠CDE=∠CED；

（2）如图，过点A作CB⊥AE于B，根据折叠的性质可得△ACF≌△ACD，可得CF=CD，∠DAC=∠FAC=60°，S△ACF=S△ACD，根据等腰三角形“三线合一”的性质可得BD=DE=，可得AB的长，利用∠DAC的三角函数可求出CB的长，根据S四边形AECF= 2S△ACD+S△ADE即可得答案．

（1），

是等边三角形

，

在△CAD和△CBE中，，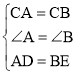

∴△CAD≌△CBE，

∴CD=CE，

∴∠CDE=∠CED．

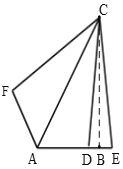
（2）如图，过点C作CB⊥AE于B，

∵将沿折叠，得到，点的对应点恰好落在AE边上，

∴△ACF≌△ACD，

∴CF=CD，∠DAC=∠FAC=60°，S△ACF=S△ACD，

∵CE=CF，

∴CD=CE，

∵CB⊥DE，DE=1，

∴BD=BE=DE=，

∵AD=3，

∴AB=AD+BD=，

∴BC=AB·tan∠DAC=×tan60°=，

∴S四边形AECF= 2S△ACD+S△ADE=2×AD·BC+DE·BC=，

故答案为：