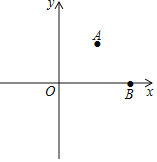题目内容
【题目】如图,已知![]() 是△
是△![]() 的外角
的外角![]() 的平分线,交
的平分线,交![]() 的延长线于点
的延长线于点![]() ,延长
,延长![]() 交△
交△![]() 的外接圆于点
的外接圆于点![]() ,连接
,连接![]() ,
, ![]() .
.
(![]() )求证:
)求证: ![]() .
.
(![]() )已知
)已知![]() ,若
,若![]() 是△
是△![]() 外接圆的直径,
外接圆的直径, ![]() ,求
,求![]() 的长.
的长.

【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:
(1)由四边形AFBC内接于圆可证得∠DAC=∠FBC;由AD平分∠EAC可得∠EAD=∠DAC,结合∠EAD=∠FAB,∠FAB=∠FCB,可得∠FCB=∠DAC,从而可得结论:∠FBC=∠FCB;
(2)由已知条件易证△ABF∽△BDF,由此可得: ![]() 即
即![]() ,从而可解得
,从而可解得![]() ;
; ![]() ,
, ![]() 可解得:FD=6,AD=4;由AB是△ABC外接圆的直径可得∠DFB=∠ACB=∠ACD=90°,由此可解得BD=
可解得:FD=6,AD=4;由AB是△ABC外接圆的直径可得∠DFB=∠ACB=∠ACD=90°,由此可解得BD=![]() ,结合∠D=∠D,可证得△DBF∽△DAC,由此可得CD:DF=AD:BD即可解得CD的值.
,结合∠D=∠D,可证得△DBF∽△DAC,由此可得CD:DF=AD:BD即可解得CD的值.
试题解析:
(![]() )∵四边形
)∵四边形![]() 内接于圆,
内接于圆,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() 是△
是△![]() 的外角
的外角![]() 平分线,
平分线,
∴![]() ,
, ![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() .
.
(![]() )由(
)由(![]() )得
)得![]() ,
,
又∵![]() ,
,
∴△![]() ∽△
∽△![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
, ![]() ,
,
∵![]() 是直径,
是直径,
∴![]() ,
,
∴BD=![]() ,
,
又∵∠D=∠D,
∴△DBF∽△DAC,
∴![]() ,
,
∴![]() CD=24,解得:CD=
CD=24,解得:CD=![]() .
.

练习册系列答案
相关题目