��Ŀ����
����Ŀ����֪����ͼ1���ȱ���ABC�ڽ��ڡ�O����P�ǡ�AB�ϵ�����һ�㣬����PA��PB��PC����D��PC��һ�㣬����DB��
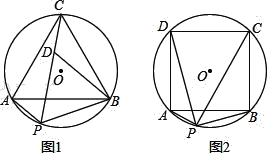
(1) ��PD=PB�����PBD�Ķ�����
(2)��(1)�������£�С��̽��![]() ��ֵ������ΪֻҪŪ��PA+PB��PC�Ĺ�ϵ���ɣ�����˼·���������¿�ͼ��ʾ��
��ֵ������ΪֻҪŪ��PA+PB��PC�Ĺ�ϵ���ɣ�����˼·���������¿�ͼ��ʾ��

����С����˼·��������������д�����̽�����̣������![]() ��ֵ��
��ֵ��
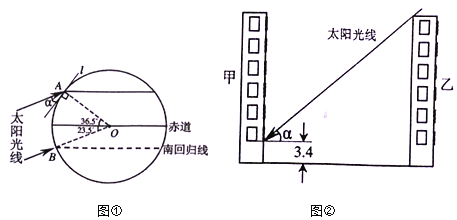
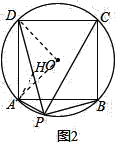
(3)��ͼ2�����������ȱ���ABC����Ϊ��������ABCD���������������䣬�ж�![]() �Ƕ�ֵ�����ǣ���������ֵ�������ǣ���˵�����ɣ�
�Ƕ�ֵ�����ǣ���������ֵ�������ǣ���˵�����ɣ�
���𰸡���1��֤������������2��![]() ����3��
����3��![]()
��������
��1�����õȱ������ε��������ж����ɵ�֤��
��2����ͨ�����߽DZߡ�֤����PBA�ա�DBC����PA=CD����PC=CD+PD=PA+PB��Ȼ��������⼴�ɣ�
��3�����������ε�����ͨ�����߽DZߡ�֤����PAB�ա�HAD����PB=DH����PD=DH+PH=PB+![]() PA��ͬ����֤�� PC=PA+
PA��ͬ����֤�� PC=PA+![]() PB����ɵ�PC+PD=��1+
PB����ɵ�PC+PD=��1+![]() ����PA+PB����Ȼ������������㼴��.
����PA+PB����Ȼ������������㼴��.
�⣺(1)�ߡ�ABC�ǵȱ������Σ�
��BA=BC����BAC=��ABC=60����
�ߡ�BPD=��CAB=60����PD=PB��
���PDB�ǵȱ������Σ�
���PBD=��ABC=60����
(2)�ߡ�PBD=��ABC=60��
���PBA=��DBC��
��BP=BD��BA=BC��
���PBA�ա�DBC��SAS����
��PA=CD��
��PC=CD+PD=PA+PB��
��![]() ��
��
(3)��ͼ2�У�����OA��OD����AH��AP��PD�ڵ�H��
���ı���ABCD�������Σ�
��AD=AB����DAB=90������AOD=90����
����APD=![]() ��AOD=45�㣬AH��PA��
��AOD=45�㣬AH��PA��
���PAH=90������AHP=��APH=45����
��AH=AP��
�ߡ�PAH=��BAD=90����
���PAB=��HAD��
���PAB�ա�HAD��SAS����
��PB=DH��
��PD=DH+PH=PB+![]() PA��
PA��
ͬ����֤��PC=PA+![]() PB��
PB��
��PC+PD=��1+![]() ����PA+PB����
����PA+PB����
��![]() .
.

����Ŀ���л�������ԴԶ�������л����֣�Ԣ����㣬Ϊ�˴������㴫ͳ�Ļ���ijУ��ί��֯��һ��ȫУ3000��ѧ���μӵ���������д�����������������в���ѧ���ijɼ���������50�֣�Ϊ�˸��õ��˽Ȿ�δ����ijɼ��ֲ�����������ȡ������200��ѧ���ijɼ����ɼ�xȡ�������ܷ�100�֣���Ϊ���������������õ����в�������ͳ��ͼ����
�ɼ�x/�� | Ƶ�� | Ƶ�� |
50��x��60 | 10 | 0.05 |
60��x��70 | 20 | 0.10 |
70��x��80 | 30 | b |
80��x��90 | a | 0.30 |
90��x��100 | 80 | 0.40 |
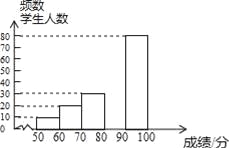
�����������Ϣ������������⣺
��1��a=______��b=______��
��2���벹ȫƵ���ֲ�ֱ��ͼ��
��3����α����ɼ�����λ��������_____________�����Σ�
��4�����ɼ���90�����ϣ�����90�֣���Ϊ�������ȣ����У�μ���α�����3000��ѧ���гɼ���������Լ�ж����ˣ�