Question

【题目】如图所示，△ABC中，AH⊥BC于H，E，D，F分别是AB，BC，AC的中点，则四边形EDHF是（ ）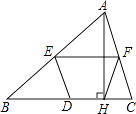
A.一般梯形
B.等腰梯形
C.直角梯形
D.直角等腰梯形

Answer 1

【答案】B
【解析】解：在△ABC中，E，F分别是AB，AC的中点，∴EF= BC，∴EF∥BC，又∵E，D分别是AB，BC的中点，∴ED= AC，
∵AH⊥BC，F是AC的中点，∴HF= AC，
∴ED=HF，
∵EF∥DH，ED=HF且ED不平行HF，
∴四边形EDHF是等腰梯形，
故选B．
【考点精析】关于本题考查的三角形中位线定理和等腰梯形的判定，需要了解连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半；两腰相等的梯形是等腰梯形；同一底上的两个角相等的梯形是等腰梯形；两条对角线相等的梯形是等腰梯形才能得出正确答案．