题目内容
【题目】如图，DE是△ABC的中位线，延长DE到F，使EF=DE，连接BF 
（1）求证：BF=DC；
（2）求证：四边形ABFD是平行四边形．
【答案】
（1）证明：连接DB，CF，
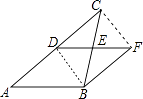
∵DE是△ABC的中位线，
∴CE=BE，
∵EF=ED，
∴四边形CDBF是平行四边形，
∴CD=BF
（2）证明：∵四边形CDBF是平行四边形，
∴CD∥FB，
∴AD∥BF，
∵DE是△ABC的中位线，
∴DE∥AB，
∴DF∥AB，
∴四边形ABFD是平行四边形
【解析】（1）连接DB，CF，利用对角线互相平分的四边形是平行四边形可得四边形CDBF是平行四边形，进而可得CD=BF；（2）由（1）可得CD∥FB，再利用三角形中位线定理可得DF∥AB，根据两组对边分别平行的四边形是平行四边形可得结论．
【考点精析】利用三角形中位线定理和平行四边形的判定对题目进行判断即可得到答案，需要熟知连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半；两组对边分别平行的四边形是平行四边形：两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形．
【题目】某校举行“汉字听写”比赛，每位学生听写汉字39个，比赛结束后，随机抽查部分学生的听写结果，以下是根据抽查结果绘制的统计图的一部分．
根据以上信息解决下列问题：
组别 | 正确字数x | 人数 |
A | 0≤x＜8 | 10 |
B | 8≤x＜16 | 15 |
C | 16≤x＜24 | 25 |
D | 24≤x＜32 | m |
E | 32≤x＜40 | 20 |
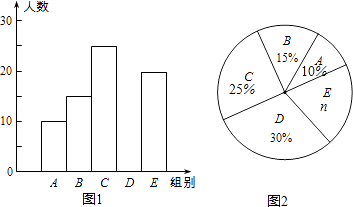
（1）在统计表中，m= ， n= ， 并补全直方图；
（2）扇形统计图中“C组”所对应的圆心角的度数是度；
（3）若该校共有964名学生，如果听写正确的个数少于24个定为不合格，请你估算这所学校本次比赛听写不合格的学生人数．
【题目】为了了解某地七年级男生的身高情况，从当地某学校选取了一个容量为60的样本，60名男生的身高(单位：cm)情况如下表所示(尚不完整)，则表中a，b的值分别为( )
分组 | 147.5～157.5 | 157.5～167.5 | 167.5～177.5 | 177.5～187.5 |
频数 | 10 | 26 | a | |
百分比 | 30% | b |
A. 18，6 B. 30%，6 C. 18，10% D. 0.3，10%