题目内容
我们知道三角形三条中线的交点叫做三角形的重心.经过证明我们可得三角形重心具备下面的性质:重心到顶点的距离与重心到该顶点对边中点的距离之比为2﹕1.请你用此性质解决下面的问题.已知:如图,点O为等腰直角三角形ABC的重心,∠CAB=90°,直线m过点O,过A、B、C三点分别作直线m的垂线,垂足分别为点D、E、F.
(1)当直线m与BC平行时(如图1),请你猜想线段BE、CF和AD三者之间的数量关系并证明;
(2)当直线m绕点O旋转到与BC不平行时,分别探究在图2、图3这两种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段AD、BE、CF三者之间又有怎样的数量关系?请写出你的结论,不需证明.
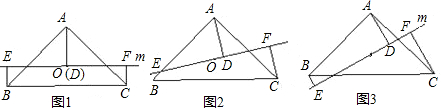
分析:(1)延长AO交BC于M点,由O为等腰直角三角形ABC的重心可得AO=2MO;再通过证明BCFE为矩形,可得BE=MO=CF,即可得AD=EB+CF;
(2)连接AO并延长交BC于点G,过G做GH⊥EF于H,由重心可得AO=2MO;再通过证明△AOD∽△GOH得AD=2HG;然后证得H为EF的中点,据中位线定理HG=
(EB+CF),即可得AD=EB+CF;
(3)图3不成立,CF-BE=AD.
(2)连接AO并延长交BC于点G,过G做GH⊥EF于H,由重心可得AO=2MO;再通过证明△AOD∽△GOH得AD=2HG;然后证得H为EF的中点,据中位线定理HG=
| 1 |
| 2 |
(3)图3不成立,CF-BE=AD.
解答:(1)猜想:BE+CF=AD(1分)
证明:如图,延长AO交BC于M点,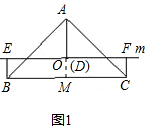
∵点O为等腰直角三角形ABC的重心
∴AO=2OM且AM⊥BC
又∵EF∥BC∴AM⊥EF
∵BE⊥EF,CF⊥EF
∴EB∥OM∥CF
∴EB=OM=CF
∴EB+CF=2OM=AD.(3分)
(2)图2结论:BE+CF=AD
证明:连接AO并延长交BC于点G,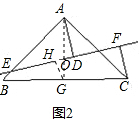
过G做GH⊥EF于H,
由重心性质可得AO=2OG,
∵∠ADO=∠OHG=90°,∠AOD=∠HOG,
∴△AOD∽△GOH,
∴AD=2HG,(5分)
∵O为重心,
∴G为BC中点,
∵GH⊥EF,BE⊥EF,CF⊥EF,
∴EB∥HG∥CF,
∴H为EF中点,
∴HG=
(EB+CF),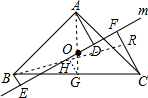
∴EB+CF=AD(7分)
(3)连接AO并延长交BC于点G,AO=2OG,
过G做GH⊥EF于H,再连接BH并延长交CF于R,
得△BEH≌△RFH(AAS),
所以CR=CF-BE=2HG=AD.
证明:如图,延长AO交BC于M点,

∵点O为等腰直角三角形ABC的重心
∴AO=2OM且AM⊥BC
又∵EF∥BC∴AM⊥EF
∵BE⊥EF,CF⊥EF
∴EB∥OM∥CF
∴EB=OM=CF
∴EB+CF=2OM=AD.(3分)
(2)图2结论:BE+CF=AD
证明:连接AO并延长交BC于点G,

过G做GH⊥EF于H,
由重心性质可得AO=2OG,
∵∠ADO=∠OHG=90°,∠AOD=∠HOG,
∴△AOD∽△GOH,
∴AD=2HG,(5分)
∵O为重心,
∴G为BC中点,
∵GH⊥EF,BE⊥EF,CF⊥EF,
∴EB∥HG∥CF,
∴H为EF中点,
∴HG=
| 1 |
| 2 |

∴EB+CF=AD(7分)
(3)连接AO并延长交BC于点G,AO=2OG,
过G做GH⊥EF于H,再连接BH并延长交CF于R,
得△BEH≌△RFH(AAS),
所以CR=CF-BE=2HG=AD.
点评:本题主要考查三角形相似的判定及性质,涉及到中位线定理、重心的性质、矩形的性质等知识点,正确作出辅助线是解题的关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目

 我们知道,任何一个三角形的三条内角平分线相交于一点,如图,若△ABC 的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.
我们知道,任何一个三角形的三条内角平分线相交于一点,如图,若△ABC 的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.

 ;
; 的最大值.
的最大值.