��Ŀ����
 ����֪�����κ�һ�������ε������ڽ�ƽ�����ཻ��һ�㣬��ͼ������ABC �������ڽ�ƽ�����ཻ�ڵ�I����I��DE��AI�ֱ�AB��AC�ڵ�D��E��
����֪�����κ�һ�������ε������ڽ�ƽ�����ཻ��һ�㣬��ͼ������ABC �������ڽ�ƽ�����ཻ�ڵ�I����I��DE��AI�ֱ�AB��AC�ڵ�D��E����1������ͨ����ͼ����������д���ϱ���ͼ���ڲݸ�ֽ�ϣ���������ȷ��
��2�����ϱ����㷢���ˡ�BIC���BDI֮���к�������ϵ����д��������˵�����еĵ�����
| ��BAC�Ķ��� | 40�� | 60�� | 90�� | 120�� |
| ��BIC�Ķ��� | ||||
| ��BDI�Ķ��� |
��������1��ͨ����ͼ��������������ɱ���
��2���ȴ��ϱ��з��֡�BIC=��BDI���ٷֱ�֤����BIC=90��+
��BAC����BDI=90��+
��BAC��
��2���ȴ��ϱ��з��֡�BIC=��BDI���ٷֱ�֤����BIC=90��+
| 1 |
| 2 |
| 1 |
| 2 |
����⣺��1����д�������£�

��2����BIC=��BDI���������£�
�ߡ�ABC�������ڽ�ƽ�����ཻ�ڵ�I��
���BIC=180��-����IBC+��ICB��
=180��-
����ABC+��ACB��
=180��-
��180��-��BAC��
=90+
��BAC��
��AIƽ�֡�BAC��
���DAI=
��DAE��
��DE��AI��I��
���AID=90�㣮
���BDI=��AID+��DAI=90��+
��BAC��
���BIC=��BDI��
| ��BAC�Ķ��� | 40�� | 60�� | 90�� | 120�� |
| ��BIC�Ķ��� | 110�� | 120�� | 135�� | 150�� |
| ��BDI�Ķ��� | 110�� | 120�� | 135�� | 150�� |

��2����BIC=��BDI���������£�
�ߡ�ABC�������ڽ�ƽ�����ཻ�ڵ�I��
���BIC=180��-����IBC+��ICB��
=180��-
| 1 |
| 2 |
=180��-
| 1 |
| 2 |
=90+
| 1 |
| 2 |
��AIƽ�֡�BAC��
���DAI=
| 1 |
| 2 |
��DE��AI��I��
���AID=90�㣮
���BDI=��AID+��DAI=90��+
| 1 |
| 2 |
���BIC=��BDI��
������������Ҫ�����������ε����ĵ����ʣ��������ڽǺͶ�������ǵ����ʣ���ƽ���ߵ������Լ����ߵ����ʣ��Ƚϼ�

��ϰ��ϵ�д�
�����Ŀ
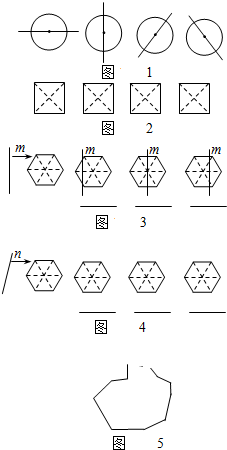 ��2013•����һģ������֪��������Բ�����ĶԳ�ͼ�Σ����Թ�Բ�ĵ��κ�һ��ֱ�߶����Խ�Բ�ָ�������ȵ������֣���ͼ1����
��2013•����һģ������֪��������Բ�����ĶԳ�ͼ�Σ����Թ�Բ�ĵ��κ�һ��ֱ�߶����Խ�Բ�ָ�������ȵ������֣���ͼ1���� ����֪�����κ�һ�������ε������ڽ�ƽ�����ཻ��һ�㣬��ͼ������ABC �������ڽ�ƽ�����ཻ�ڵ�I����I��DE��AI�ֱ�AB��AC�ڵ�D��E��
����֪�����κ�һ�������ε������ڽ�ƽ�����ཻ��һ�㣬��ͼ������ABC �������ڽ�ƽ�����ཻ�ڵ�I����I��DE��AI�ֱ�AB��AC�ڵ�D��E��




