题目内容
(2013•鼓楼区一模)问题提出:
规定:四条边对应相等,四个角对应相等的两个四边形全等.
我们借助学习“三角形全等的判定”获得的经验与方法对“全等四边形的判定”进行探究.
初步思考:
在两个四边形中,我们把“一条边对应相等”或“一个角对应相等”称为一个条件.满足4个条件的两个四边形不一定全等,如边长相等的正方形与菱形就不一定全等.类似地,我们容易知道两个四边形全等至少需要5个条件.
深入探究:
小莉所在学习小组进行了研究,她们认为5个条件可分为以下四种类型:
Ⅰ一条边和四个角对应相等;Ⅱ二条边和三个角对应相等;
Ⅲ三条边和二个角对应相等;Ⅳ四条边和一个角对应相等.
(1)小明认为“Ⅰ一条边和四个角对应相等”的两个四边形不一定全等,请你举例说明.
(2)小红认为“Ⅳ四条边和一个角对应相等”的两个四边形全等,请你结合下图进行证明.
已知:如图,
求证:
证明:
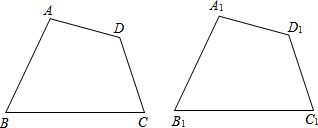
(3)小刚认为还可以对“Ⅱ二条边和三个角对应相等”进一步分类,他以四边形ABCD和四边形A1B1C1D1为例,分为以下几类:
①AB=A1B1,AD=A1D1,∠A=∠A1,∠B=∠B1,∠C=∠C1;
②AB=A1B1,AD=A1D1,∠A=∠A1,∠B=∠B1,∠D=∠D1;
③AB=A1B1,AD=A1D1,∠B=∠B1,∠C=∠C1,∠D=∠D1;
④AB=A1B1,CD=C1D1,∠A=∠A1,∠B=∠B1,∠C=∠C1.
其中能判定四边形ABCD和四边形A1B1C1D1全等的是
(4)小亮经过思考认为也可以对“Ⅲ三条边和二个角对应相等”进一步分类,请你仿照小刚的方法先进行分类,再概括得出一个全等四边形的判定方法.
规定:四条边对应相等,四个角对应相等的两个四边形全等.
我们借助学习“三角形全等的判定”获得的经验与方法对“全等四边形的判定”进行探究.
初步思考:
在两个四边形中,我们把“一条边对应相等”或“一个角对应相等”称为一个条件.满足4个条件的两个四边形不一定全等,如边长相等的正方形与菱形就不一定全等.类似地,我们容易知道两个四边形全等至少需要5个条件.
深入探究:
小莉所在学习小组进行了研究,她们认为5个条件可分为以下四种类型:
Ⅰ一条边和四个角对应相等;Ⅱ二条边和三个角对应相等;
Ⅲ三条边和二个角对应相等;Ⅳ四条边和一个角对应相等.
(1)小明认为“Ⅰ一条边和四个角对应相等”的两个四边形不一定全等,请你举例说明.
(2)小红认为“Ⅳ四条边和一个角对应相等”的两个四边形全等,请你结合下图进行证明.
已知:如图,
四边形ABCD和四边形A1B1C1D1中,AB=A1B1,BC=B1C1,CD=C1D1,DA=D1A1,∠B=∠B1.
四边形ABCD和四边形A1B1C1D1中,AB=A1B1,BC=B1C1,CD=C1D1,DA=D1A1,∠B=∠B1.
.求证:
四边形ABCD≌四边形A1B1C1D1
四边形ABCD≌四边形A1B1C1D1
.证明:

(3)小刚认为还可以对“Ⅱ二条边和三个角对应相等”进一步分类,他以四边形ABCD和四边形A1B1C1D1为例,分为以下几类:
①AB=A1B1,AD=A1D1,∠A=∠A1,∠B=∠B1,∠C=∠C1;
②AB=A1B1,AD=A1D1,∠A=∠A1,∠B=∠B1,∠D=∠D1;
③AB=A1B1,AD=A1D1,∠B=∠B1,∠C=∠C1,∠D=∠D1;
④AB=A1B1,CD=C1D1,∠A=∠A1,∠B=∠B1,∠C=∠C1.
其中能判定四边形ABCD和四边形A1B1C1D1全等的是
①②③
①②③
(填序号),概括可得“全等四边形的判定方法”,这个判定方法是有一组邻边和三个角对应相等的两个四边形全等
有一组邻边和三个角对应相等的两个四边形全等
.(4)小亮经过思考认为也可以对“Ⅲ三条边和二个角对应相等”进一步分类,请你仿照小刚的方法先进行分类,再概括得出一个全等四边形的判定方法.
分析:(1)可以利用正方形与矩形进行说明;
(2)根据四条边对应相等,和一个角对应相等,结合图形即可写出已知与求证.证明时可以连接AC、A1 C1,转化为证明△ABC≌△A1 B1 C1,和△AC D≌△A1 B1 C1.即可征得;
(3)根据条件能证明△ABC≌△A1 B1 C1,和△AC D≌△A1 B1 C1,的条件.
(4)写出三条边对应相等,和二个角对应相等分情况进行讨论即可.
(2)根据四条边对应相等,和一个角对应相等,结合图形即可写出已知与求证.证明时可以连接AC、A1 C1,转化为证明△ABC≌△A1 B1 C1,和△AC D≌△A1 B1 C1.即可征得;
(3)根据条件能证明△ABC≌△A1 B1 C1,和△AC D≌△A1 B1 C1,的条件.
(4)写出三条边对应相等,和二个角对应相等分情况进行讨论即可.
解答:解:(1)如正方形与矩形有一条边对应相等,但显然不一定全等.
(2)已知:如图,四边形ABCD和四边形A1 B1 C1 D1中,AB=A1 B1,BC=B1 C1,CD=C1 D1,DA=D1A1,∠B=∠B1.
求证:四边形ABCD≌四边形A1 B1 C1 D1.
证明:连接AC、A1 C1.
∵AB=A1 B1,∠B=∠B1,BC=B1 C1,
∴△ABC≌△A1 B1 C1.
∴AC=A1 C1,∠BAC=∠B1 A1 C1,
∠BCA=∠B1 C1A1.
又∵CD=C1 D1,DA=D1A1,
∴△AC D≌△A1 B1 C1.
∴∠D=∠D1.
∴∠BAD=∠B1 A1 D1,∠BCD=∠B1 C1 D1.
∴四边形ABCD≌四边形A1 B1 C1 D1
(3)①②③;
有一组邻边和三个角对应相等的两个四边形全等.
(4)分为四类:
①AB=A1B1,BC=B1C1,CD=C1D1,∠A=∠A1,∠B=∠B1;
②AB=A1B1,BC=B1C1,CD=C1D1,∠A=∠A1,∠C=∠C1;
③AB=A1B1,BC=B1C1,CD=C1D1,∠A=∠A1,∠D=∠D1;
④AB=A1B1,BC=B1C1,CD=C1D1,∠B=∠B1,∠C=∠C1.
有三条边和这三条边中每一组邻边的夹角对应相等的两个四边形全等.
(2)已知:如图,四边形ABCD和四边形A1 B1 C1 D1中,AB=A1 B1,BC=B1 C1,CD=C1 D1,DA=D1A1,∠B=∠B1.
求证:四边形ABCD≌四边形A1 B1 C1 D1.

证明:连接AC、A1 C1.
∵AB=A1 B1,∠B=∠B1,BC=B1 C1,
∴△ABC≌△A1 B1 C1.
∴AC=A1 C1,∠BAC=∠B1 A1 C1,
∠BCA=∠B1 C1A1.
又∵CD=C1 D1,DA=D1A1,
∴△AC D≌△A1 B1 C1.
∴∠D=∠D1.
∴∠BAD=∠B1 A1 D1,∠BCD=∠B1 C1 D1.
∴四边形ABCD≌四边形A1 B1 C1 D1
(3)①②③;
有一组邻边和三个角对应相等的两个四边形全等.
(4)分为四类:
①AB=A1B1,BC=B1C1,CD=C1D1,∠A=∠A1,∠B=∠B1;
②AB=A1B1,BC=B1C1,CD=C1D1,∠A=∠A1,∠C=∠C1;
③AB=A1B1,BC=B1C1,CD=C1D1,∠A=∠A1,∠D=∠D1;
④AB=A1B1,BC=B1C1,CD=C1D1,∠B=∠B1,∠C=∠C1.
有三条边和这三条边中每一组邻边的夹角对应相等的两个四边形全等.
点评:本题考查了多边形的全等,多边形的全等可以通过作辅助线转化为证明三角形全等问题.

练习册系列答案
相关题目