Question

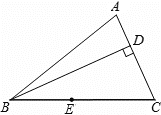
【题目】如图，矩形ABCD的顶点AB在x轴上，点D的坐标为（6，8），点E在边BC上，△CDE沿DE翻折后点C恰好落在x轴上点F处，若△ODF为等腰三角形，点E的坐标为 ．

Answer 1

【答案】（16，3）或（4+6，2﹣2）或（，）．

【解析】

试题分析：先依据勾股定理求得OD=10，①当OD=DF时，由勾股定理可求得AF=6，故此可求得OF=12，由翻折的性质可知DC=10，从而得到点E的横坐标为16，FB=4，最后在Rt△EFB中，依据勾股定理列方程求解即可；②当OD=OF时．先求得AF=4，由勾股定理可求得DF=4，从而得到点E的横坐标为6+4，FB=4﹣4，最后在Rt△EFB中，依据勾股定理列方程求解即可；③当OF=DF时，设点F的坐标为（b，0），依据两点间的距离公式列出关于b的方程可求得b=．即OF=，从而得到AF=，依据勾股定理可求得DF=，从而得到点E的横坐标为，BF=6，最后在Rt△EFB中，依据勾股定理列方程求解即可．

解：∵点D的坐标为（6，8），

∴OD=10．

①当OD=DF=10时．

∵DF=10，AD=8，

∴AF=6．

∴OF=12．

由翻折的性质可知：DC=DF=10，FE=CE，

∴点E的横坐标为16．

∴FB=4．

设点E的纵坐标为a，则FE=8﹣a．

在Rt△EFB中，FB2+BE2=FE2，即42+a2=（8﹣a）2，解得a=3．

∴点E的坐标为（16，3）．

②当OD=OF时．

∵OF=10，0A=6，

∴AF=4．

∵在Rt△DAF中，DF==4．

∴点E的横坐标为6+4．

∴FB=4﹣4．

设点E的纵坐标为a，则FE=8﹣a．

在Rt△EFB中，FB2+BE2=FE2，即（4﹣4）2+a2=（8﹣a）2，解得a=2﹣2．

∴点E的坐标为（4+6，2﹣2）．

③当OF=DF时，设点F的坐标为（b，0），则82+（b﹣6）2=b2．解得：b=．即OF=．

∵OA=6，OF=，

∴AF=．

∴DF==．

由翻折的性质可知：DC=DF，则点E的横坐标为+6=．

在Rt△EFB中，FB2+BE2=FE2，即（﹣）2+a2=（8﹣a）2，解得a=．

∴点E的坐标为（，）．

综上所述，点E的坐标为（16，3）或（4+6，2﹣2）或（，）．

故答案为：（16，3）或（4+6，2﹣2）或（，）．