Question

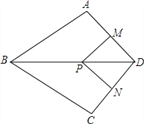
【题目】如图，直线AB与CD相交于点O，OE⊥CD．

（1）若∠BOD=28°，求∠AOE的度数．

（2）若OF平分∠AOC，小明经探究发现：当∠BOD为锐角时，∠EOF的度数始终都是∠BOC度数的一半，请你判断他的发现是否正确，并说明理由．

Answer 1

【答案】（1）62°；（2）正确，

【解析】试题分析：（1）根据对顶角相等求出∠AOC的度数，根据垂直的定义计算即可；

（2）设∠BOD=x，用x表示出∠AOC和∠BOC，根据邻补角的概念计算即可；

试题解析：

（1）∵∠BOD=28°，

∴∠AOC=∠BOD=28°，

∵OE⊥CD，

∴∠EOC=90°，

∴∠AOE=∠EOC﹣∠AOC=62°；

（2）正确，

设∠BOD=x，则∠AOC=∠BOD=x，∠BOC=180°﹣x，

∵OF平分∠AOC，

∴∠FOC=x，

∴∠EOF=90°﹣∠FOC=90°﹣x，

∴∠EOF=∠BOC．