题目内容
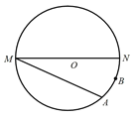
【题目】如图,MN是⊙O的直径,MN=4,点A在⊙O上,∠AMN=30°,B为![]() 的中点,P是直径MN上一动点,则PA+PB的最小值为_____.
的中点,P是直径MN上一动点,则PA+PB的最小值为_____.
【答案】![]()
【解析】
作点A关于MN的对称点A′,连接A′B,与MN的交点即为点P,此时PA+PB的最小值即为A′B的长,连接OA′、OB、OA,先求∠A′OB=∠A′ON+∠BON=60°+30°=90°,再根据勾股定理即可得出答案.
解:作点A关于MN的对称点A′,连接A′B,与MN的交点即为点P,PA+PB的最小值即为A′B的长,连接OA′、OB、OA,
∵A′点为点A关于直线MN的对称点,∠AMN=30°,
∴∠AON=∠A′ON=2∠AMN=2×30°=60°,
又∵B为![]() 的中点, ∴
的中点, ∴![]() ,
,
∴∠BON=∠AOB=![]() ∠AON=
∠AON=![]() ×60°=30°,
×60°=30°,
∴∠A′OB=∠A′ON+∠BON=60°+30°=90°,
又∵MN=4, ∴OA′=OB=![]() MN=
MN=![]() ×4=2,
×4=2,
∴Rt△A′OB中,A′B=![]() ,
,
即PA+PB的最小值为![]() .
.

故答案为:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某市将实行居民生活用电阶梯电价方案,如下表,图中折线反映了每户居民每月电费![]() (元)与用电量
(元)与用电量![]() (度)间的函数关系.
(度)间的函数关系.
档次 | 第一档 | 第二档 | 第三档 |
每月用电量 |
|
|
|
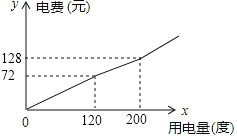
(1)小王家某月用电![]() 度,需交电费___________元;
度,需交电费___________元;
(2)求第二档电费![]() (元)与用电量
(元)与用电量![]() (度)之间的函数关系式;
(度)之间的函数关系式;
(3)小王家某月用电![]() 度,交纳电费
度,交纳电费![]() 元,请你求出第三档每度电费比第二档每度电费多多少元?
元,请你求出第三档每度电费比第二档每度电费多多少元?