题目内容
【题目】对于平面直角坐标系![]() O
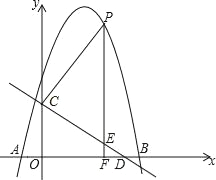
O![]() 中的点P和⊙C,给出如下定义:若⊙C上存在两个点M,N,使得∠MPN=60°,则称P为⊙C 的关联点。已知点D(
中的点P和⊙C,给出如下定义:若⊙C上存在两个点M,N,使得∠MPN=60°,则称P为⊙C 的关联点。已知点D(![]() ,
,![]() ),E(0,-2),F(
),E(0,-2),F(![]() ,0)
,0)
(1)当⊙O的半径为1时,
①在点O,D,E,F中,⊙O的关联点是______ ____;
②如果G(0,t)是⊙O的关联点,则t的取值范围是 ;
(2)如果线段EF上每一个点都是⊙O的关联点,那么⊙O的半径![]() 最小为 ;
最小为 ;
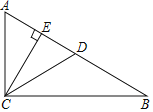
(3)Rt⊿ABC中,∠C=90![]() ,BC=8,∠A=30
,BC=8,∠A=30![]() ,⊙P的半径为1,当点P运动时,始终确保⊿ABC的三条边中至少有一条边上恰好有唯一的⊙P的关联点。请你画出点P所走过的路线围成的图形的示意图,并在下面横线上直接写出它的总长。
,⊙P的半径为1,当点P运动时,始终确保⊿ABC的三条边中至少有一条边上恰好有唯一的⊙P的关联点。请你画出点P所走过的路线围成的图形的示意图,并在下面横线上直接写出它的总长。

答:点P经过的路线围成的图形的总长为 。
【答案】(1)①O、D、E;②-2≤t≤2;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)①根据关联点的定义得出E点是 O的关联点,进而得出F、D,与 O的关系;
②根据题意可知G(0,t)是⊙O的关联点,计算出t的取值范围即可;
(2)若线段EF上的所有点都是某个圆的关联点,欲使这个圆的半径最小,则这个圆的圆心应在线段EF的中点;再考虑临界情况,即恰好E、F点为 K的关联时,则KF=2KN=![]() EF=2,即可得出圆的半径r的取值范围,即可得出结论.
EF=2,即可得出圆的半径r的取值范围,即可得出结论.
(3)根据题意与周长公式列出等式即可得出结论.
(1)① O、D、E
② -2≦t≦2
根据关联点的定义得出E点是 O的关联点,根据题意可知G(0,t)是⊙O的关联点,所以t的范围是-2≦t≦2.
(2)若线段EF上的所有点都是某个圆的关联点,欲使这个圆的半径最小,则这个圆的圆心应在线段EF的中点;再考虑临界情况,即恰好E、F点为 K的关联时,则KF=2KN=![]() EF=2,即可得出圆的半径r的取值范围,
EF=2,即可得出圆的半径r的取值范围,![]() .
.
(3)点P经过的路线围成的图形的总长为![]() .
.