题目内容
【题目】已知关于x的方程x2+（m﹣3）x﹣m（2m﹣3）=0
（1）证明：无论m为何值方程都有两个实数根；
（2）是否存在正数m，使方程的两个实数根的平方和等于26？若存在，求出满足条件的正数m的值；若不存在，请说明理由．
【答案】（1）见解析；（2）
【解析】试题分析：（1）求出根的判别式，再根据非负数的性质即可证明；
（2）根据一元二次方程根与系数的关系即可求得方程两根的和与两根的积，两根的平方和可以用两根的和与两根的积表示，根据方程的两个实数根的平方和等于26，即可得到一个关于m的方程，求得m的值．
试题解析：（1）证明：∵关于x的方程x2+（m﹣3）x﹣m（2m﹣3）=0的判别式△=（m﹣3）2+4m（2m﹣3）=9（m﹣1）2≥0，∴无论m为何值方程都有两个实数根；
（2）解：设方程的两个实数根为x1、x2，则x1+x2=﹣（m﹣3），x1×x2=﹣m（2m﹣3），令x12+x22=26，得：（x1+x2）2﹣2x1x2=（m﹣3）2+2m（2m﹣3）=26，整理得：5m2﹣12m﹣17=0，解这个方程得：m= 
或m=﹣1，所以存在正数m= 
，使得方程的两个实数根的平方和等于26．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
【题目】已知
是
的函数，自变量的取值范围为
，下表是与的几组对应值
| 0 | 1 | 2 | 3 | 3.5 | 4 | 4.5 | … |
| 1 | 2 | 3 | 4 | 3 | 2 | 1 | … |
小明根据学习函数的经验，利用上述表格所反映出的与之间的变化规律，对该函数的图象与性质进行了探究.下面是小明的探究过程，请补充完整：
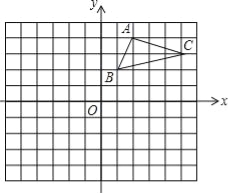
(1)如图，在平面直角坐标系中，指出了以上表中各对对应值为坐标的点. 根据描出的点，画出该函数的图象.
(2)根据画出的函数图象填空.
①该函数图象与轴的交点坐标为_____.
②直接写出该函数的一条性质.
