题目内容
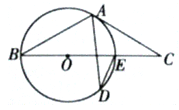
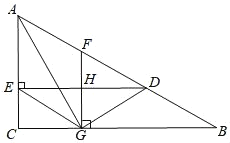
【题目】如图，
中，
，DE垂直平分AB，交线段BC于点E（点E与点C不重合），点F为AC上一点，点G为AB上一点（点G与点A不重合），且
．
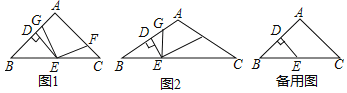
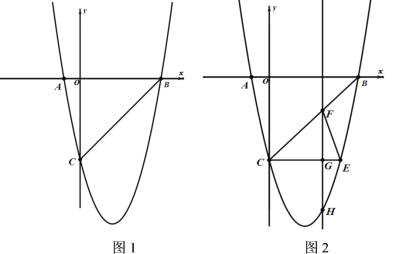
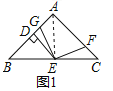
（1）如图1，当
时，线段AG和CF的数量关系是 ．
（2）如图2，当
时，猜想线段AG和CF的数量关系，并加以证明．
（3）若
，
，
，请直接写出CF的长．
【答案】（1）
；（2）
，理由见解析；（3）2.5或5
【解析】
（1）如图1，连接AE，根据线段垂直平分线的性质得到
，根据等腰直角三角形的性质得到
，
，
，根据全等三角形的性质即可得到结论；
（2）如图2，连接AE，根据等腰三角形的性质和三角形的内角和得到
，根据线段垂直平分线的性质得到，求得
，根据相似三角形的性质得到
，解直角三角形即可得到；
（3）①当G在DA上时，如图3，连接AE，根据线段垂直平分线的性质得到
，，由三角函数的定义得到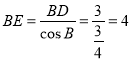
，根据相似三角形的性质得到
，过A作
于点H由三角函数的定义即可得到结论．②当点G在BD上，如图4，方法同（1）．
解：（1）相等，理由：如图1，连接AE，
∵DE垂直平分AB，
，
，
，
，
，，
，
，
，
，
，
，
；
故答案为：；
（2），
理由：如图2，连接AE，
，
，
，
∵DE垂直平分AB，
，
，
，
，
，
，
，
，
，
，
在
中，
，
，
，
；
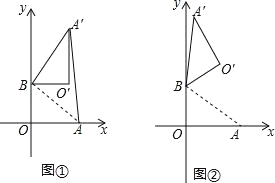
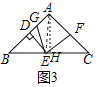
（3）①当G在DA上时，如图3，连接AE，
∵DE垂直平分AB，
，，
，
，
，
，
，
，
，
，
，
，
，
，
，
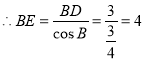过A作于点H，
，
，
，
，
，
，
，
，
；
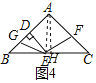
②当点G在BD上，如图4，同（1）可得，
，
，
，
，
，
综上所述，CF的长为2.5或5．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
