Question

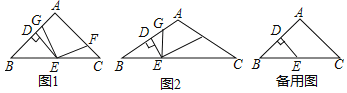
【题目】如图，△ABC中，D是AB上一点，DE⊥AC于点E，F是AD的中点，FG⊥BC于点G，与DE交于点H，若FG＝AF，AG平分∠CAB，连接GE，GD．

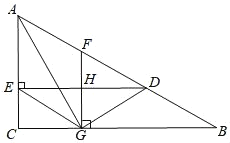
（1）求证：△ECG≌△GHD；

（2）小亮同学经过探究发现：AD＝AC+EC．请你帮助小亮同学证明这一结论．

（3）若∠B＝30°，判定四边形AEGF是否为菱形，并说明理由．

Answer 1

【答案】（1）见解析；（2）见解析；（3）是菱形，证明见解析

【解析】

（1）依据条件得出∠C=∠DHG=90°，∠CGE=∠GED，依据F是AD的中点，FG∥AE，即可得到FG是线段ED的垂直平分线，进而得到GE=GD，∠CGE=∠GDE，利用AAS即可判定△ECG≌△GHD；（注：本小题也可以通过证明四边形ECGH为矩形得出结论）.

（2）过点G作GP⊥AB于P，判定△CAG≌△PAG，可得AC=AP，由（1）可得EG=DG，即可得到Rt△ECG≌Rt△DPG，依据EC=PD，即可得出AD=AP+PD=AC+EC；

（3）依据∠B=30°，可得∠ADE=30°，进而得到AE=AD，故AE=AF=FG，再根据四边形AEGF是平行四边形，即可得到四边形AEGF是菱形．

解：（1）∵AF＝FG，

∴∠FAG＝∠FGA，

∵AG平分∠CAB，

∴∠CAG＝∠FAG，

∴∠CAG＝∠FGA，

∴AC∥FG，

∵DE⊥AC，

∴FG⊥DE，

∵FG⊥BC，

∴DE∥BC，

∴AC⊥BC，

∴∠C＝∠DHG＝90°，∠CGE＝∠GED，

∵F是AD的中点，FG∥AE，

∴H是ED的中点，

∴FG是线段ED的垂直平分线，

∴GE＝GD，∠GDE＝∠GED，

∴∠CGE＝∠GDE，

∴△ECG≌△GHD；

（2）证明：过点G作GP⊥AB于P，

∴GC＝GP，而AG＝AG，

∴△CAG≌△PAG，

∴AC＝AP，

由（1）可得EG＝DG，

∴Rt△ECG≌Rt△DPG，

∴EC＝PD，

∴AD＝AP+PD＝AC+EC；

（3）四边形AEGF是菱形，

证明：∵∠B＝30°，

∴∠ADE＝30°，

∴AE＝AD，

∴AE＝AF＝FG，

由（1）得AE∥FG，

∴四边形AEGF是平行四边形，

∵AE＝AF，

∴四边形AEGF是菱形．