题目内容
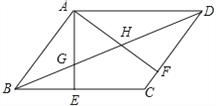
【题目】如图，在平行四边形ABCD中，AE⊥BC于E，AF⊥CD于F，BD与AE、AF交于G、H．
（1）求证：△ABE∽△ADF；
（2）若AG=AH，求证：四边形ABCD是菱形．
【答案】（1）证明见解析；（2）菱形，证明见解析.
【解析】试题分析：（1）根据平行四边形的对角相等，以及垂直的定义可得△ABE和△ADF的两角对应相等，则两个三角形相似；
（2）证明△ABG≌△ADH，则AB=AD，从而证得四边形是菱形．
试题解析：（1）证明：∵AE⊥BC，AF⊥CD，
∴∠AEB=∠AFD=90°，
∵四边形ABCD是平行四边形，
∴∠ABE=∠ADF，
∴△ABE∽△ADF（有两角相等的三角形是相似三角形）
（2）∵△ABE∽△ADF，
∴∠BAG=∠DAH，
∵AG=AH，
∴∠AGH=∠AHG，
从而∠AGB=∠AHD，
∴△ABG≌△ADH（ASA），
∴AB=AD，
∵四边形ABCD是平行四边形，
∴四边形ABCD是菱形（一组邻边相等的平行四边形是菱形）
练习册系列答案
优生乐园系列答案
新编小学单元自测题系列答案
相关题目
