题目内容
【题目】如图,四边形OABC是菱形,若OA=2,∠AOC=45°,则B点的坐标是 ( )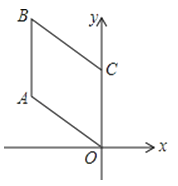
A.(﹣2,2+![]() )
)
B.(2,2+![]() )
)
C.(-![]() , 2+
, 2+![]() )
)
D.(![]() , 2+
, 2+![]() )
)
【答案】C
【解析】解:作BF⊥y轴于F,如图所示:
则∠BFC=90°,
∵四边形OABC是菱形,
∴OC=OA=CB=2,BC∥OA,
∴∠BCF=∠AOC=45°,
∴△BCF是等腰直角三角形,
∴BF=CF=BC×![]() =
=![]() ,
,
∴OF=2+![]() ,
,
∴B点的坐标是:(﹣![]() , 2+
, 2+![]() );
);
故选:C.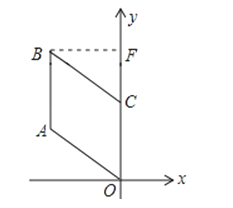
作BF⊥y轴于F,则∠BFC=90°,由菱形的性质得出OC=OA=CB=2,BC∥OA,得出∠BCF=∠AOC=45°,△BCF是等腰直角三角形,根据三角函数求出BF=CF,得出OF,即可得出B点坐标.
【考点精析】掌握菱形的性质是解答本题的根本,需要知道菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目