题目内容
 已知:如图,在⊙O中,CD过圆心O,且CD⊥AB,垂足为D,过点C任作一弦CF交⊙O于F,交AB于E.求证:CB2=CF•CE.
已知:如图,在⊙O中,CD过圆心O,且CD⊥AB,垂足为D,过点C任作一弦CF交⊙O于F,交AB于E.求证:CB2=CF•CE.
 证明:连接FB,
证明:连接FB,∵CD过圆心O,且CD⊥AB,
∴
 =
=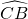 .
.∴∠CBE=∠F.
∵∠BCE为公共角,
∴△CBE∽△CFB.
∴
 =
= .
.∴CB2=CE•CF.
分析:连接BF,证所求的对应边成比例线段所在的三角形相似即可,即证△CBE∽△CFB.
点评:此题考查了垂径定理及相似三角形的判定和性质.

练习册系列答案
相关题目
 24、已知:如图,在?ABCD中,对角线AC交BD于点O,四边形AODE是平行四边形.求证:四边形ABOE、四边形DCOE都是平行四边形.
24、已知:如图,在?ABCD中,对角线AC交BD于点O,四边形AODE是平行四边形.求证:四边形ABOE、四边形DCOE都是平行四边形. 21、已知:如图,在△ABC中,AB=AC,点D,E在边BC上,且BD=CE.
21、已知:如图,在△ABC中,AB=AC,点D,E在边BC上,且BD=CE. (1)计算:
(1)计算: 点A重合.将线段AP绕点A逆时针旋转到AQ,使∠PAQ=∠BAC,连接BP,CQ
点A重合.将线段AP绕点A逆时针旋转到AQ,使∠PAQ=∠BAC,连接BP,CQ (2012•密云县一模)已知:如图,在△ABC中,∠A=∠B=30°,D是AB 边上一点,以AD为直径作⊙O恰过点C.
(2012•密云县一模)已知:如图,在△ABC中,∠A=∠B=30°,D是AB 边上一点,以AD为直径作⊙O恰过点C.