题目内容
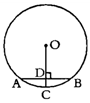
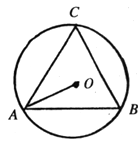
如图,在Rt△ABC中,∠ACB=90°,AC=6㎝,BC=8㎝,P为BC的中点.动点Q从点P出发,沿射线PC方向以2㎝/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s.
⑴当t=1.2时,判断直线AB与⊙P的位置关系,并说明理由;
⑵已知⊙O为△ABC的外接圆,若⊙P与⊙O相切,求t的值.
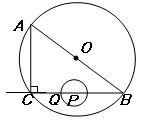
⑴当t=1.2时,判断直线AB与⊙P的位置关系,并说明理由;
⑵已知⊙O为△ABC的外接圆,若⊙P与⊙O相切,求t的值.

解:⑴直线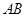 与⊙P相切.
与⊙P相切.
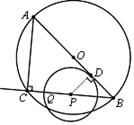
如图,过点P作PD⊥AB, 垂足为D.
在Rt△ABC中,∠ACB=90°,∵AC=6cm,BC=8cm,
∴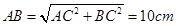 .∵P为BC的中点,∴PB=4cm.
.∵P为BC的中点,∴PB=4cm.
∵∠PDB=∠ACB=90°,∠PBD=∠ABC.∴△PBD∽△ABC.
∴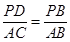 ,即
,即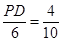 ,∴PD ="2.4(cm)" .
,∴PD ="2.4(cm)" .
当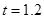 时,
时,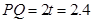 (cm)
(cm)
∴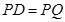 ,即圆心
,即圆心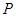 到直线
到直线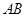 的距离等于⊙P的半径.
的距离等于⊙P的半径.
∴直线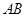 与⊙P相切.
与⊙P相切.
⑵∠ACB=90°,∴AB为△ABC的外切圆的直径.∴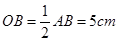 .
.
连接OP.∵P为BC的中点,∴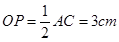 .
.
∵点P在⊙O内部,∴⊙P与⊙O只能内切.
∴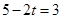 或
或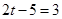 ,∴
,∴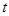 =1或4.
=1或4.
∴⊙P与⊙O相切时,t的值为1或4.
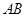 与⊙P相切.
与⊙P相切.
如图,过点P作PD⊥AB, 垂足为D.
在Rt△ABC中,∠ACB=90°,∵AC=6cm,BC=8cm,
∴
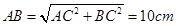 .∵P为BC的中点,∴PB=4cm.
.∵P为BC的中点,∴PB=4cm.∵∠PDB=∠ACB=90°,∠PBD=∠ABC.∴△PBD∽△ABC.
∴
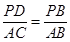 ,即
,即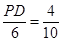 ,∴PD ="2.4(cm)" .
,∴PD ="2.4(cm)" .当
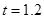 时,
时,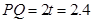 (cm)
(cm) ∴
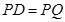 ,即圆心
,即圆心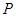 到直线
到直线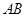 的距离等于⊙P的半径.
的距离等于⊙P的半径. ∴直线
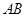 与⊙P相切.
与⊙P相切.⑵∠ACB=90°,∴AB为△ABC的外切圆的直径.∴
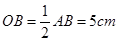 .
.连接OP.∵P为BC的中点,∴
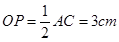 .
. ∵点P在⊙O内部,∴⊙P与⊙O只能内切.
∴
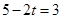 或
或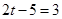 ,∴
,∴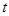 =1或4.
=1或4. ∴⊙P与⊙O相切时,t的值为1或4.
本试题主要是考查了圆内的性质的运用,以及直线与圆的为何只关系 的综合运用。
(1)当t=1.2时,要判断直线AB与⊙P的位置关系,只要求解圆心到直线的距离与圆的半径的关系即可以得到。
(2)⊙O为△ABC的外接圆,若⊙P与⊙O相切,则可以考虑是相互外切还是相互内切的情况,根据圆心距和半径的关系得到
(1)当t=1.2时,要判断直线AB与⊙P的位置关系,只要求解圆心到直线的距离与圆的半径的关系即可以得到。
(2)⊙O为△ABC的外接圆,若⊙P与⊙O相切,则可以考虑是相互外切还是相互内切的情况,根据圆心距和半径的关系得到

练习册系列答案
相关题目

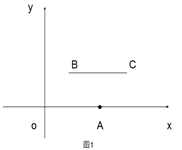
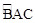 的中点,连接PA、PB、PC、PD,当BD的长度为多少时,△PAD是以AD为底边的等腰三角形?并加以证明。
的中点,连接PA、PB、PC、PD,当BD的长度为多少时,△PAD是以AD为底边的等腰三角形?并加以证明。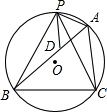
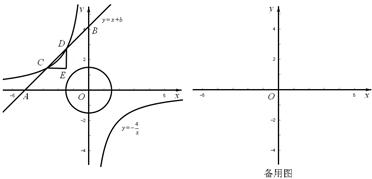
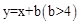 与x轴、y轴分别相交于点A、B,与正比例函数
与x轴、y轴分别相交于点A、B,与正比例函数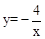 的图象相交于点C、D(点C在点D的左侧),⊙O是以CD长为半径的圆。CE∥x轴,DE∥y轴,CE、DE相交于点E。
的图象相交于点C、D(点C在点D的左侧),⊙O是以CD长为半径的圆。CE∥x轴,DE∥y轴,CE、DE相交于点E。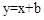 与⊙O有哪些位置关系?求出相应b的取值范围。
与⊙O有哪些位置关系?求出相应b的取值范围。