题目内容
【题目】如图,AB为半圆O的直径,AD、BC分别切⊙O于A、B两点,CD切⊙O于点E,AD与CD相交于D,BC与CD相交于C,连接OD、OC,对于下列结论:
①OD2=DECD;②AD+BC=CD;③OD=OC;④S梯形ABCD=![]() CDOA;⑤∠DOC=90°,
CDOA;⑤∠DOC=90°,
其中正确的是_____.(只需填上正确结论的序号)

【答案】①②⑤
【解析】
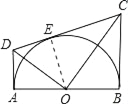 如图,连接OE,
如图,连接OE,
∵DA、DE为圆O的切线,
∴AD=ED,∠AOD=∠EOD,
∵CE、CB为圆O的切线,
∴CE=CB,∠EOC=∠BOC,
同理,AD=DE,∠AOD=∠EOC,
∴CD=DE+EC=AD+BC,选项②正确;
∴S梯形ABCD=![]() CDAB,选项④错误;
CDAB,选项④错误;
∵∠AOD+∠DOE+∠EOC+∠BOC=180°,
∴∠DOE+∠EOC=90°,即∠DOC=90°,选项⑤正确;
∵OE⊥CD,
∴∠OED=∠COD=90°,
∵∠EDO=∠ODC,
∴△DOE∽△CDE,
∴OD2=DECD,选项①正确;
故答案为:①②⑤.

练习册系列答案
相关题目






