��Ŀ����
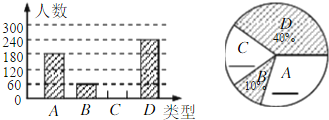
����Ŀ��ij�̵����ۼס���������Ʒ������������Ϣ��

����������Ϣ������������⣺
��1����ס���������Ʒ�Ľ������ۣ�
��2����֪�ס���������Ʒ�����۵��۷ֱ�Ϊ2Ԫ��3Ԫ�����̵�ƽ��ÿ����������Ʒ500��������Ʒ1300�������г����鷢�֣�������Ʒ���۵���ÿ��0.1Ԫ��������Ʒÿ��ɶ�����100�����̵�����Ѽ�����Ʒ�����۵����½�m��m��0��Ԫ���ڲ������������ص������£���mΪ��ֵʱ���̵�ÿ�����ۼס���������Ʒ��ȡ��������Ϊ1800Ԫ��ע����������=���۵��۩��������ۣ�
���𰸡���1������Ʒ��������Ϊ1Ԫ������Ʒ��������Ϊ2Ԫ����2����m=0.5ʱ���̵��ȡ��������Ϊ1800Ԫ��
��������
�����������1������ͼ����Ϣ���Եó�������Ʒ֮��۸�֮��ĵ�����ϵ�����ɵó�������������ɣ�
��2�����ݽ��ۺ��ÿ����������500+![]() ��100������ÿ�����ۺ�ÿ������Ϊ����1��m��Ԫ�����ɵó�����������һԪ���η��̽ⷨ������ɣ�
��100������ÿ�����ۺ�ÿ������Ϊ����1��m��Ԫ�����ɵó�����������һԪ���η��̽ⷨ������ɣ�
�⣺��1�������Ʒ��������xԪ������Ʒ��������yԪ��
�����⣬��
![]()
��ã�![]() ��
��
�𣺼���Ʒ��������Ϊ1Ԫ������Ʒ��������Ϊ2Ԫ��
��2�������⣬��
��2��m��1����500+1000m��+��3��2����1300=1800
��1��m����500+1000m��=500
��2m2��m=0
��m1=0.5��m2=0
��m��0
��m=0������ȥ����m=0.5
�𣺵�m=0.5ʱ���̵��ȡ��������Ϊ1800Ԫ��