题目内容
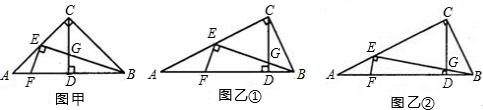
已知:在△ABC中∠ACB=90°,CD⊥AB于点D,点E在AC上,BE交CD于点G,EF⊥BE交AB于点F.如图甲,当AC=BC时,且CE=EA时,则有EF=EG;
(1)如图乙①,当AC=2BC时,且CE=EA时,则线段EF与EG的数量关系是:EF
(2)如图乙②,当AC=2BC时,且CE=2EA时,请探究线段EF与EG的数量关系,并证明你的结论;
(3)当AC=mBC时且CE=nEA时,则线段EF与EG的数量关系,并直接写出你的结论(不用证明).
分析:本题需要寻找相似三角形,并利用相似三角形的性质依次推理得出结论.
解答: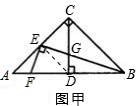 图甲:连接DE,
图甲:连接DE,
∵AC=BC,CD⊥AB,
∴AD=BD,∠ACD=45°,
∴CD=AD=
AB,
∵AE=EC,
∴DE=AE=EC=
AC,
∴∠EDC=45°,DE⊥AC,
∵∠A=45°,
∴∠A=∠EDG,
∵EF⊥BE,
∵∠AEF+∠FED=∠EFD+∠DEG=90°,
∴∠AEF=∠DEG,
∴△AEF≌△DEG(ASA),
∴EF=EG.
(1)EF=
EG;
(2)解:EF=
EG.
证明:作EM⊥AB于点M,EN⊥CD于点N,
∵EM∥CD,
∴△AEM∽△ACD,
∴
=
=
即EM=
CD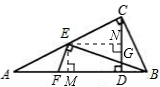 ,
,
同理可得,EN=
AD,
∵∠ACB=90°,CD⊥AB,
∴tanA=
=
=
,
∴
=
=
=
•
=
×
=
,
又∵EM⊥AB,EN⊥CD,
∴∠EMF=∠ENG=90°,
∵EF⊥BE,
∴∠FEM=∠GEN,
∴△EFM∽△EGN,
∴
=
=
,
即EF=
EG;
(3)由(1)当AC=2BC时,且CE=EA时,EF=
EG,
当AC=2BC时,且CE=2EA时,EF=
EG,
可以得出:当AC=mBC时且CE=nEA时,EF=
EG.
 图甲:连接DE,
图甲:连接DE,∵AC=BC,CD⊥AB,
∴AD=BD,∠ACD=45°,
∴CD=AD=
| 1 |
| 2 |
∵AE=EC,
∴DE=AE=EC=
| 1 |
| 2 |
∴∠EDC=45°,DE⊥AC,
∵∠A=45°,
∴∠A=∠EDG,
∵EF⊥BE,
∵∠AEF+∠FED=∠EFD+∠DEG=90°,
∴∠AEF=∠DEG,
∴△AEF≌△DEG(ASA),
∴EF=EG.
(1)EF=
| 1 |
| 2 |
(2)解:EF=
| 1 |
| 4 |
证明:作EM⊥AB于点M,EN⊥CD于点N,
∵EM∥CD,
∴△AEM∽△ACD,
∴
| EM |
| CD |
| AE |
| AC |
| 1 |
| 3 |
即EM=
| 1 |
| 3 |
 ,
,同理可得,EN=
| 2 |
| 3 |
∵∠ACB=90°,CD⊥AB,
∴tanA=
| CD |
| AD |
| BC |
| AC |
| 1 |
| 2 |
∴
| EM |
| EN |
| ||
|
| CD |
| 2AD |
| 1 |
| 2 |
| CD |
| AD |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
又∵EM⊥AB,EN⊥CD,
∴∠EMF=∠ENG=90°,
∵EF⊥BE,
∴∠FEM=∠GEN,
∴△EFM∽△EGN,
∴
| EF |
| EG |
| EM |
| EN |
| 1 |
| 4 |
即EF=
| 1 |
| 4 |
(3)由(1)当AC=2BC时,且CE=EA时,EF=
| 1 |
| 2 |
当AC=2BC时,且CE=2EA时,EF=
| 1 |
| 4 |
可以得出:当AC=mBC时且CE=nEA时,EF=
| 1 |
| mn |
点评:本题关键是要懂得找相似三角形,利用相似三角形的性质求解,难度较大.

练习册系列答案
相关题目
 25、已知:在△ABC中AB=AC,点D在CB的延长线上.
25、已知:在△ABC中AB=AC,点D在CB的延长线上. (1)化简:(a-
(1)化简:(a- 20、如图,已知,在△ABC中,∠ABC和∠ACB的平分线交于点M,ME∥AB交BC于点E,MF∥AC交BC于点F.求证:△MEF的周长等于BC的长.
20、如图,已知,在△ABC中,∠ABC和∠ACB的平分线交于点M,ME∥AB交BC于点E,MF∥AC交BC于点F.求证:△MEF的周长等于BC的长. 12、已知,在△ABC中,AB=AC=x,BC=6,则腰长x的取值范围是
12、已知,在△ABC中,AB=AC=x,BC=6,则腰长x的取值范围是
 已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足为点E.∠B=38°,∠C=70°.
已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足为点E.∠B=38°,∠C=70°.