题目内容
20、如图，已知，在△ABC中，∠ABC和∠ACB的平分线交于点M，ME∥AB交BC于点E，MF∥AC交BC于点F．求证：△MEF的周长等于BC的长．分析：要证△MEF的周长为ME+EF+FM=BE+EF+FC=BC．由BM平分∠ABC，CM平分∠ACB，ME∥AB，MF∥AC，
可知△BEM和△CFM为等腰三角形，故ME=BE，MF=CF即证．
可知△BEM和△CFM为等腰三角形，故ME=BE，MF=CF即证．
解答：证明：∵BM平分∠ABC，CM平分∠ACB，ME∥AB，MF∥AC，
∴∠MBE=∠BME，∠FMC=∠FCM．
∴△BEM和△CFM为等腰三角形．
∴ME=BE，MF=CF．
∴△MEF的周长为ME+EF+FM=BE+EF+FC=BC．
∴∠MBE=∠BME，∠FMC=∠FCM．
∴△BEM和△CFM为等腰三角形．
∴ME=BE，MF=CF．
∴△MEF的周长为ME+EF+FM=BE+EF+FC=BC．
点评：此题考查了平行线及角平分线的性质，等腰三角形的判定定理，比较简单．
练习册系列答案
相关题目
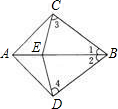
如图，已知：在Rt△ABC中，∠C=90°，E为AB的中点，且DE⊥AB于E，若∠CAD：∠DAB=1﹕2，求∠B的度数．
