题目内容
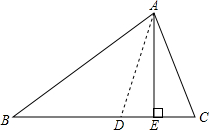 已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足为点E.∠B=38°,∠C=70°.
已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足为点E.∠B=38°,∠C=70°.①求∠DAE的度数;
②试写出∠DAE与∠B、∠C之间的一般等量关系式(只写结论)
分析:①根据三角形内角和定理求出∠BAC的度数,再根据角平分线的定义求出∠BAD,根据直角三角形两锐角互余求出∠BAE,然后求解即可;
②根据①的思路,把角的度数转化为角整理即可得解.
②根据①的思路,把角的度数转化为角整理即可得解.
解答:解:①∵∠B=38°,∠C=70°(已知),
∴∠BAC=180°-∠B-∠C=180°-38°-70°=72°,
∵AD平分∠BAC,
∴∠BAD=36°,
∵AE⊥BC,垂足为点E,
∴∠AEB=90°,
∴∠BAE=90°-38°=52°,
∴∠DAE=∠BAE-∠BAD=16°;
②∠DAE=
(∠C-∠B).
理由如下:根据三角形的内角和定理,∠BAC=180°-∠B-∠C,
∵AD平分∠BAC,
∴∠BAD=
(180°-∠B-∠C),
∵AE⊥BC,垂足为点E,
∴∠AEB=90°,
∴∠BAE=90°-∠B,
∴∠DAE=90°-∠B-
(180°-∠B-∠C),
=90°-∠B-90°+
∠B+
∠C,
=
(∠C-∠B).
∴∠BAC=180°-∠B-∠C=180°-38°-70°=72°,
∵AD平分∠BAC,
∴∠BAD=36°,
∵AE⊥BC,垂足为点E,
∴∠AEB=90°,
∴∠BAE=90°-38°=52°,
∴∠DAE=∠BAE-∠BAD=16°;
②∠DAE=
| 1 |
| 2 |
理由如下:根据三角形的内角和定理,∠BAC=180°-∠B-∠C,
∵AD平分∠BAC,
∴∠BAD=
| 1 |
| 2 |
∵AE⊥BC,垂足为点E,
∴∠AEB=90°,
∴∠BAE=90°-∠B,
∴∠DAE=90°-∠B-
| 1 |
| 2 |
=90°-∠B-90°+
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
点评:本题考查了三角形的内角和定理,角平分线的定义,三角形的高线的定义,准确识图并熟记定理与定义是解题的关键.

练习册系列答案
相关题目
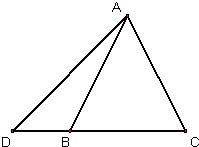 25、已知:在△ABC中AB=AC,点D在CB的延长线上.
25、已知:在△ABC中AB=AC,点D在CB的延长线上.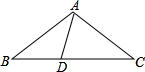 (1)化简:(a-
(1)化简:(a- 20、如图,已知,在△ABC中,∠ABC和∠ACB的平分线交于点M,ME∥AB交BC于点E,MF∥AC交BC于点F.求证:△MEF的周长等于BC的长.
20、如图,已知,在△ABC中,∠ABC和∠ACB的平分线交于点M,ME∥AB交BC于点E,MF∥AC交BC于点F.求证:△MEF的周长等于BC的长.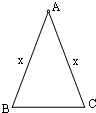 12、已知,在△ABC中,AB=AC=x,BC=6,则腰长x的取值范围是
12、已知,在△ABC中,AB=AC=x,BC=6,则腰长x的取值范围是