题目内容
25、已知：在△ABC中AB=AC，点D在CB的延长线上．求证：AD2-AB2=BD•CD．
分析：可过点A作BC的垂线，利用直角三角形中斜边与直角边的关系，进而可求解．
解答：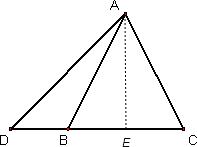
证明：如图，过点A作AE⊥BC，
∵AB=AC，
∴BE=CE（三线合一），
在Rt△ADE中，AD2=AE2+DE2，
在Rt△ABE中，AB2=AE2+BE2，
∴AD2-AB2=AE2+DE2-AE2-BE2=DE2-BE2=（DE+BE）•（DE-BE）=CD•BD
即AD2-AB2=BD•CD．
证明：如图，过点A作AE⊥BC，∵AB=AC，
∴BE=CE（三线合一），
在Rt△ADE中，AD2=AE2+DE2，
在Rt△ABE中，AB2=AE2+BE2，
∴AD2-AB2=AE2+DE2-AE2-BE2=DE2-BE2=（DE+BE）•（DE-BE）=CD•BD
即AD2-AB2=BD•CD．
点评：熟练掌握直角三角形中勾股定理的运用，能够解决一些简单的证明问题．
练习册系列答案
相关题目
（1）化简：（a-
20、如图，已知，在△ABC中，∠ABC和∠ACB的平分线交于点M，ME∥AB交BC于点E，MF∥AC交BC于点F．求证：△MEF的周长等于BC的长．
12、已知，在△ABC中，AB=AC=x，BC=6，则腰长x的取值范围是
已知：在△ABC中，∠B＜∠C，AD平分∠BAC，AE⊥BC，垂足为点E．∠B=38°，∠C=70°．