ƒøƒ⁄»ð
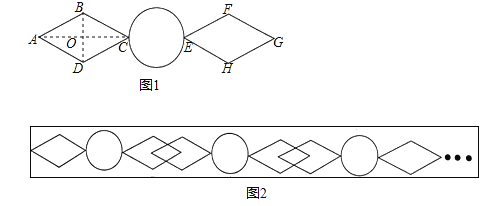
°æƒø°ø∫œ∑ –¥Ú‘Ï ¿ΩÁº∂π˙º“¬√”Œ÷––ƒ£¨æ´–ƒ…˺∆12∏ˆ«ßƒÍπ≈’Ú°£»ÁÕº1 «ƒ≥√˜«Â–°‘∫Œß«Ω÷–µƒæ´√¿Õº∞∏£¨À¸ «¡Ω∏ˆ–Œ◊¥¥Û–°œýÕ¨µƒ¡‚–Œ”Γª∏ˆ‘≤◊È≥…£¨«“A°¢C°¢E°¢G‘⁄∆‰∂‘≥∆÷·AG…œ.“—÷™¡‚–Œµƒ±þ≥§∫Õ‘≤µƒ÷±æ∂∂º «1dm£¨°œA= 60°„.

£®1£©«ÛÕº∞∏÷–AGµƒ≥§£ª
£®2£©ºŸ…Ë–°‘∫µƒŒß«Ω“ª≤ý”√…œ ˆÕº∞∏»ÁÕº2≈≈¡–£¨∆‰÷–µ⁄∂˛øÈÕº∞∏◊Û±þ¡‚–Œ“ª∏ˆ∂•µ„’˝∫√æ≠π˝µ⁄“ªøÈÕº∞∏µƒ”“±þ¡‚–Œµƒ∂‘≥∆÷––ƒ£¨....,“‘¥À¿ýÕ∆£¨µ⁄101øÈ’‚÷÷Õº∞∏’‚—˘≈≈¡–≥§Œ™∂ý…Ÿm£ø£®≤ªøº¬«∑Ïœ∂º∞∆¥Ω”¥¶£©

°æ¥∞∏°ø£®1£©AG=(![]() )dm£ª£®2£©
)dm£ª£®2£©![]() m
m
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫£®1£©¡¨Ω”BD£¨ACΩª”⁄O£¨”…”⁄Àƒ±þ–ŒABCD «¡‚–Œ£¨µ√µΩAC°ÕBD£¨Ω‚÷±Ω«»˝Ω«–Œµ√µΩAO=![]() £¨”⁄ «µ√µΩΩ·¬€£ª
£¨”⁄ «µ√µΩΩ·¬€£ª
£®2£©∏˘æð“‚µ√£¨AG=![]() £¨”⁄ «µ√µΩŒß«Ω“ª≤ý≈≈¡–nøȵƒ◊Ð≥§
£¨”⁄ «µ√µΩŒß«Ω“ª≤ý≈≈¡–nøȵƒ◊Ð≥§![]() +£®n©Å1£©£®
+£®n©Å1£©£®![]() +1£©£¨º¥ø…µ√µΩΩ·¬€£Æ
+1£©£¨º¥ø…µ√µΩΩ·¬€£Æ
‘Ã‚Ω‚Œˆ£∫Ω‚£∫£®1£©¡¨Ω”BD£¨ACΩª”⁄O£Æ°þÀƒ±þ–ŒABCD «¡‚–Œ£¨°ýAC°ÕBD£Æ°þAB=1£¨°œA=60°„£¨°ý°œBAO=30°„£¨°ýAO=![]() £¨°ýAC=
£¨°ýAC=![]() £Æ°þ‘≤µƒ÷±æ∂∂º «1dm£¨°ýAG=£®
£Æ°þ‘≤µƒ÷±æ∂∂º «1dm£¨°ýAG=£®![]() £©dm£ª
£©dm£ª
£®2£©∏˘æð“‚µ√£∫AG=![]() £¨∂¯Œß«Ω“ª≤ý≈≈¡–nøȵƒ◊Ð≥§£∫
£¨∂¯Œß«Ω“ª≤ý≈≈¡–nøȵƒ◊Ð≥§£∫ ![]() +£®n©Å1£©£®
+£®n©Å1£©£®![]() +1£©£¨°ýµ⁄101øÈ’‚÷÷Õº∞∏’‚—˘≈≈¡–≥§Œ™
+1£©£¨°ýµ⁄101øÈ’‚÷÷Õº∞∏’‚—˘≈≈¡–≥§Œ™![]() +£®101©Å1£©£®
+£®101©Å1£©£®![]() +1£©=£®
+1£©=£®![]() £©dm=
£©dm=![]() √◊£Æ
√◊£Æ

 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏






