Question

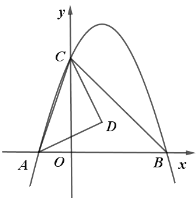
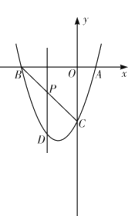
【题目】如图，抛物线与轴交于两点，于轴交于点，连接，已知．

（1）求抛物线的解析式；

（2）点是线段上一动点，过点P作轴，交抛物线于点D，求的长的最大值；

（3）若点E是轴上一点，以为顶点的三角形是腰三角形，求点的坐标．

Answer 1

【答案】（1）；（2）；（3）点的坐标为或或或

【解析】

（1）把A，B两点坐标代入求出a，c的值即可得出结论；

（2）求出直线BC的解析式为，设设，则，从而得到，进而得到结论；

（3）分BC为底边或腰进行求解即可．

解：（1）把，分别代入，得

解得

∴抛物线的解析式为．

（2）由（1）知，抛物线的解析式为，

当时，，

∴．

设直线BC的解析式为，

把，分别代入，

得

解得

∴直线BC的解析式为．

∵点在线段BC上，点D在抛物线上，轴，

∴设，则，

∴．

∴当，即时，PD的长的值最大，

PD的长的最大值为．

（3）在中，，根据勾股定理，得

．

①若，则点是BC的垂直平分线与轴的交点，

点E与原点O重合，

∴．

②若，则，点E与点C关于原点对称，

∴．

③若，则或．

设点，则．

∴．

∴．

综上所述，以，，为顶点的三角形是等腰三角形时，点的坐标为或或或．