题目内容
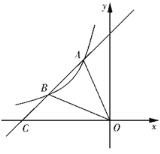
【题目】如图,已知⊙O的半径长为1,AB、AC是⊙O的两条弦,且AB=AC,BO的延长线交AC于点D,连接OA、OC.
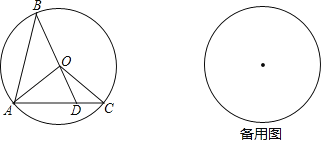
(1)求证:△OAD∽△ABD;
(2)当△OCD是直角三角形时,求B、C两点的距离;
(3)记△AOB、△AOD、△COD的面积分别为S1、S2、S3,如果S22=S1S3,试证明点D为线段AC的黄金分割点.
【答案】(1)见解析;(2)![]() 或
或![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)先判断出![]() ,即可得出结论;
,即可得出结论;
(2)分两种情况:当![]() 时,先判断出
时,先判断出![]() 是等边三角形,进而判断出
是等边三角形,进而判断出![]() ,再求出
,再求出![]() 即可得出结论;当
即可得出结论;当![]() ,利用等腰直角三角形,即可得出结论;
,利用等腰直角三角形,即可得出结论;
(3)先表示出![]() ,
,![]() ,
,![]() ,再由
,再由![]() ,得出
,得出![]() ,化简得出
,化简得出![]() ,即可得出结论.
,即可得出结论.
(1)证明:![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(2)解:![]() 是直角三角形,
是直角三角形,
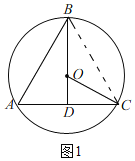
当![]() 时,连接
时,连接![]() ,如图1,
,如图1,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
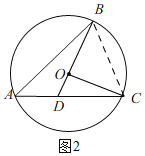
当![]() 时,连接
时,连接![]() ,如图2,
,如图2,
![]() ,
,
![]() ,
,
![]() ,
,
故![]() 、
、![]() 两点的距离为
两点的距离为![]() 或
或![]() ;
;
(3)证明:如图3,
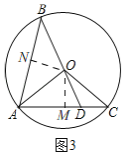
过点![]() 作
作![]() 于
于![]() ,
,![]() 于
于![]() ,
,
由(1)知,![]() ,
,
![]() ,
,
![]() 、
、![]() 、
、![]() 的面积分别为
的面积分别为![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 点
点![]() 为线段
为线段![]() 的黄金分割点.
的黄金分割点.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目