题目内容
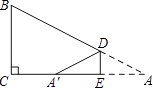
【题目】如图,在矩形ABCD中,∠B的平分线BE与AD交于点E,∠BED的平分线EF与DC交于点F,若AB=9,DF=2FC,则BC= . (结果保留根号)
【答案】![]()
【解析】解:延长EF和BC,交于点G
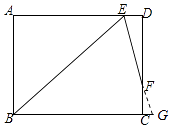
∵矩形ABCD中,∠B的角平分线BE与AD交于点E,
∴∠ABE=∠AEB=45°,
∴AB=AE=9,
∴直角三角形ABE中,BE= ![]() =
= ![]() ,
,
又∵∠BED的角平分线EF与DC交于点F,
∴∠BEG=∠DEF
∵AD∥BC
∴∠G=∠DEF
∴∠BEG=∠G
∴BG=BE= ![]()
由∠G=∠DEF,∠EFD=∠GFC,可得△EFD∽△GFC
∴ ![]()
设CG=x,DE=2x,则AD=9+2x=BC
∵BG=BC+CG
∴ ![]() =9+2x+x
=9+2x+x
解得x= ![]()
∴BC=9+2( ![]() ﹣3)=
﹣3)= ![]()
故答案为: ![]()
在矩形ABCD中,∠B的角平分线BE与AD交于点E,得到∠ABE=∠AEB=45°,AB=AE=9,直角三角形ABE中,BE= ![]() =
= ![]() ,又∠BED的角平分线EF与DC交于点F,得到∠BEG=∠DEF,由AD∥BC,得到∠G=∠DEF,∠BEG=∠G,BG=BE=
,又∠BED的角平分线EF与DC交于点F,得到∠BEG=∠DEF,由AD∥BC,得到∠G=∠DEF,∠BEG=∠G,BG=BE= ![]() ,由∠G=∠DEF,∠EFD=∠GFC,可得△EFD∽△GFC,得到
,由∠G=∠DEF,∠EFD=∠GFC,可得△EFD∽△GFC,得到 ![]() ,设CG=x,DE=2x,则AD=9+2x=BC,由BG=BC+CG,得到
,设CG=x,DE=2x,则AD=9+2x=BC,由BG=BC+CG,得到 ![]() =9+2x+x,解得x=
=9+2x+x,解得x= ![]() ,得到BC=9+2(
,得到BC=9+2( ![]() ﹣3)=
﹣3)= ![]()

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目