��Ŀ����
����Ŀ��������������1��3��5��7��9��11������һ�������ų����±���
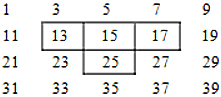
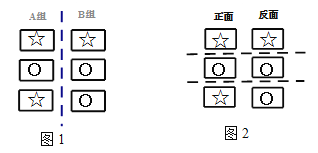
ͼ�е�![]() �ֿ��ס���ĸ���������
�ֿ��ס���ĸ���������![]() �ֿ����������ƶ�����ͬ���ķ�ʽ�ɿ�ס������ĸ���.
�ֿ����������ƶ�����ͬ���ķ�ʽ�ɿ�ס������ĸ���.
��1�������д�С�������еĵ�9������17����40������______����100������______����![]() ������______��
������______��
��2����![]() �ֿ��ڴ����м��ҿ��Ϸ����������������д�С�������еĵ�
�ֿ��ڴ����м��ҿ��Ϸ����������������д�С�������еĵ�![]() �����������ú�
�����������ú�![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() �ֿ��е��ĸ����ĺͣ�
�ֿ��е��ĸ����ĺͣ�
��3������![]() �ֿ����������ƶ�����ס���ĸ����ĺ��ܵ���406�����ܣ�������ĸ������粻�ܣ�˵������.
�ֿ����������ƶ�����ס���ĸ����ĺ��ܵ���406�����ܣ�������ĸ������粻�ܣ�˵������.
���𰸡���1��79��199 ��![]() ����2��
����2��![]() ����3����ס���ĸ����ĺͲ��ܵ���406
����3����ס���ĸ����ĺͲ��ܵ���406
��������
��1�����ݱ������ݹ��ɼ��ɵó��𰸣�
��2����T�ֿ��ڴ����м��ҿ��Ϸ�����Ϊ2n1������ڸ�����ߵ���Ϊ2n3���ұߵ�Ϊ2n��1���������Ϊ2n1��10���ɵó�T�ֿ����ĸ����ĺͣ�
��3����������8n��6��406�����n��50����2n1��99�����������ĵ�10�е����ұߣ������ܴ���T�ֿ����м��ҿ��Ϸ��������ʿ�ס���ĸ����ĺͲ��ܵ���406��
��1��������������1��3��5��7��������
���40������40��21��79����100������100��21��199����n������2n1��
�ʴ�Ϊ��79��199��2n1��
��2�������⣬��T�ֿ��ڴ����м��ҿ��Ϸ�����Ϊ2n1��
����ڸ�����ߵ���Ϊ2n3���ұߵ�Ϊ2n��1���������Ϊ2n1��10��
��T�ֿ����ĸ����ĺ�Ϊ��
2n3��2n1��2n��1��2n1��10��8n��6��
��T�ֿ����ĸ����ĺ�Ϊ��8n��6��
��3�������⣬���ס���ĸ����ĺ�Ϊ406�����У�
8n��6��406�����n��50��
������2n1��99�����������ĵ�10�е����ұߣ������ܴ���T�ֿ����м��ҿ��Ϸ����������Բ��������⣮
�ʿ�ס���ĸ����ĺͲ��ܵ���406��

 �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�